
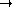 tel que l'image de 1 est . L'image de est
tel que l'image de 1 est . L'image de est mod
on donnera la réponse sous la forme du représentant entre 0 et -1.L'homomorphisme se factorise en un homomorphisme injectif
 /
/

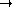
 -modules se trouvent dans
le module
OEF
-modules se trouvent dans
le module
OEF  -modules.
-modules.
L'exposant de est égal à , son cardinal est .

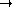 tel que l'image de 1 est . L'image de est
tel que l'image de 1 est . L'image de est mod
on donnera la réponse sous la forme du représentant entre 0 et -1.L'homomorphisme se factorise en un homomorphisme injectif
 /
/

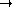
On donnera la suite des facteurs invariants sous la forme avec avec des entiers nuls ou strictement supérieurs à 1 et vérifiant .
On considère le sous-groupe de engendré par les éléments et . On désire calculer les invariants (diviseurs élémentaires) de . L'exercice comporte 3 étapes. Attention, même si vous vous trompez, cela ne vous sera dit qu'à la fin.
Donnez un homomorphisme
de
dans  tel que l'image de
soit maximale (on donnera
par sa matrice dans la base canonique
) :
tel que l'image de
soit maximale (on donnera
par sa matrice dans la base canonique
) :
On a donc avec =
Vous avez choisi
de matrice et dit que l'image de
par
est  .
Donnez un élément
de
tel que
soit dans
et tel que
dans la base (
,
) :
.
Donnez un élément
de
tel que
soit dans
et tel que
dans la base (
,
) :
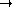 un homomorphisme de groupes . Soit
un élément de
.
un homomorphisme de groupes . Soit
un élément de
. Sans renseignement supplémentaire, que pouvez-vous affirmer (donner la réponse la plus précise) :
Si est d'ordre dans , l'ordre de dans est .
a-t-il d'éléments d'ordre ?
quel est l'ordre de la classe de ?
On peut l'écrire comme produit de groupes cycliques d'ordre une puissance d'un nombre premier (décomposition primaire). Donner la liste de leurs ordres (sans répétition)
.
Le théorème de structure dit qu'il est isomorphe à un unique groupeavec . Donner la liste des entiers .
On peut l'écrire comme produit de groupes cycliques d'ordre une puissance d'un nombre premier (décomposition primaire). Donner la liste de leurs ordres
.
Le théorème de structure dit qu'il est isomorphe à un unique groupeavec . Donner la liste des entiers .
et le sous-groupe engendré par l'image de (). On désire calculer la structure du groupe quotient . Pour cela, on considère l'homomorphisme naturel . Donner un système générateur du noyau de l'homomorphisme déduit On écrira les vecteurs de en colonnes ; sur une ligne, séparer les composantes par une virgule ; aucun calcul n'est nécessaire, on ne demande qu'un système générateur.
Un système générateur
du noyau de 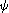 est
.
(votre réponse était fausse).
Calculer une base adaptée à
et au groupe abélien engendré par
.
est
.
(votre réponse était fausse).
Calculer une base adaptée à
et au groupe abélien engendré par
.
, ,
Donner la structure de en donnant la suite des entiers avec .
On pourra s'aider de l'égalité suivante où les matrices carrées à gauche sont de déterminant 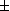 1
1
 /
/


 /
/

 /
/ 

 /
/ 
 /
/ 

 /
/ 
Il est d'ordre divisible par . Comme est abélien, il possède un sous-groupe d'ordre . Décrire un tel sous-groupe par ses générateurs.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.