OEF Géométrie affine
--- Introduction ---
Ce module regroupe pour l'instant 14 exercices sur la géométrie affine.
Il comporte un QCM présenté en deux versions :
- Dans le QCM I, vous pouvez choisir le nombre de questions proposées.
Dès qu'une réponse est fausse, l'exercice est terminé.
- Le QCM II propose trois questions. Après chacune réponse,
la bonne réponse est affichée. L'exercice est terminé après les trois questions.
Les deux versions utilisent la même liste de questions et chaque
question peut exister en plusieurs versions. Pour cette raison,
ils peuvent être renouvelés plusieurs fois.
Coordonnées barycentriques
Soient
un repère du plan Donnez les coordonnées barycentriques (
) du point
vérifiant :
Barycentre et côtés d'un triangle
Soient
un repère du plan affine. Soit
le point de coordonnées barycentriques
. On appelle
le point intersection des droites
et
. - Vérifiez que
existe.
- Déterminez le rapport
des vecteurs colinéaires .
Barycentres : lequel ?
Le barycentre des points (
; ), (
; ), (
; ) est-il
,
ou
?
xrange -2, +2 yrange -2, +2 disk ,,3,black disk ,,3,black disk ,,3,black ftriangle ,,,,,,pink polyline black,,,,,,,, text black,,+2,medium,A text black,,-1,medium,B text black,,-1,medium,C disk ,,3,purple disk ,,3,blue disk ,,3,red text purple,,,medium, text blue,,,medium, text red,,,medium,
Régions et barycentre
Cliquez dans la région dans laquelle se trouve le barycentre de
,
et
Barycentre et Céva
Soit
un repère du plan affine. On considère les points
,
et
de coordonnées barycentriques respectives :
,
,
.
Vérifiez que les droites
,
et
sont concourantes en un point
et donnez ses coordonnées barycentriques(
).
Droites affines dans l'espace
Les droites
et
de l'espace sont données par leur représentation paramétrique dans un repère affine de l'espace :
et
Les deux droites sont
Coord. barycentriques et droite
Soient
un repère du plan affine. Caractérisez sur leurs coordonnées barycentriques (
) les points de . Si une coordonnée est quelconque, entrez le mot tout.
Intersection
Consigne
Remplir les champs par une valeur numérique ou le mot "tout".
Nombre d'équations
Dans un espace affine de dimension
, quel est le nombre minimal d'équations cartésiennes d' ?
Points affinement indépendants
Soient
,
,
et
des points d'un espace La proposition suivante est-elle vraie ? Les quatre points sont affinement indépendants
n'appartient pas au sous-espace affine engendré par
,
et
.
Prolongement d'une application affine
Dans le plan affine
, on considère les points : Il existe
application(s) affine(s) de
dans lui-même qui envoi(en)t
sur
,
sur
,
sur
et
sur
.
Espaces affines : QCM I
Ce QCM comporte questions. Mais il s'arrête dès que vous avez fait une erreur.
Question k :
Votre réponse :
r[k]
La bonne réponse :
Espaces affines : QCM II
Ce QCM comporte questions. Après votre réponse à une question, la bonne réponse et la question suivante s'affichent. Vos réponses seront analysées à la fin.
Question k :
Votre réponse :
r[k]
La bonne réponse :
Sous-es. vectoriels ou affines
Dans le 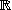 -espace vectoriel , muni de sa structure affine canonique, on considère le sous-ensemble
défini par :
-espace vectoriel , muni de sa structure affine canonique, on considère le sous-ensemble
défini par :
Que peut-on dire de
?
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur la géométrie affine. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, geometry, affine_geometry,, barycenter, théorème de ceva, coordinates
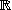 -espace vectoriel , muni de sa structure affine canonique, on considère le sous-ensemble
défini par :
-espace vectoriel , muni de sa structure affine canonique, on considère le sous-ensemble
défini par :