OEF Abscisse curviligne
--- Introduction ---
Ce module regroupe pour l'instant 13 exercices sur l'intégrale curviligne d'une fonction.
Chemin en montagne
Soit
le chemin tracé sur la montagne
d'équation
et dont la projection sur la carte est d'équations paramétriques
pour
[ ,].
Calculer la longueur du chemin sur la carte et la longueur réelle du chemin. Pour information, voici la carte :
xrange -, yrange -, trange , arrow 0,0, 0,1,10,black arrow 0,0, 1,0 ,10,black vline 0,0, black hline 0,0, black linewidth 1 levelcurve blue, , plot green,,
Intégrale curviligne d'une fonction
Soit
une fonction de classe
sur
. L'intégrale curviligne de
le long de la courbe
d'équations paramétriques
pour
[,]
se ramène à une intégrale simple :
(
,
,
) (
)1/2
.
Remplissez les blancs.
Intégrales curvilignes (en polaire)
Soit
une fonction sur
. L'intégrale curviligne de
le long de la courbe
donnée en coordonnées polaires
par l'équation
avec
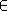
[,]
(
,
,
) (
)1/2
.
Remplissez les blancs.
Longueur et courbes de niveau
On considère une surface
d'équation
dont quelques courbes de niveau sont tracées sur le dessin : du bleu vers le rouge, les niveaux dessinés sont égaux à .
Soit d'autre part - une courbe
tracée sur la surface
et dont la projection sur le plan
est le segment d'extrémités les points
et
- la ligne polygonale
de
dont les sommets sont les points de la courbe
se projettant sur les points
du plan
qui partagent le segment
en parts égales avec
et
xrange , yrange ,
Que peut-on dire de la longueur de la courbe
la longueur de la courbe
.
Calculer la longueur de
.
Intégrales curvilignes 2
Calculer l'intégrale curviligne de la fonction
définie par
le long de la courbe
formée des segments qui joignent les points () à () et () à ( ).
Intégrales curvilignes 3D
Calculer l'intégrale curviligne de la fonction
définie sur
par
le long de la courbe
(orientée) formée des segments qui joignent les points () à () et () à ( ).
Intégrale curviligne d'une fonction 3D
Soit
une fonction de classe
sur
. L'intégrale curviligne de
le long de la courbe
d'équations paramétriques
pour
[, ]
se ramène à une intégrale simple :
(
,
,
,
,
,
,
) (
)1/2
.
Remplissez les blancs.
Intégrale curviligne d'une fonction 3D
Soit
une fonction de classe
sur
. L'intégrale curviligne de
le long de la courbe
d'équations paramétriques
pour
[, ]
se ramène à une intégrale simple :
(
,
,
,
,
,
,
) (
)1/2
.
Remplissez les blancs.
Longueur d'une courbe
Soit
la courbe tracée sur la surface
d'équation
et dont la projection sur le plan
est d'équations paramétriques
pour
[ ,].
Calculer la longueur de la projection de
et la longueur de la courbe
.
Pour information, voici quelques courbes de niveau de la surface en bleu et la projection de la courbe
en vert.
xrange -, yrange -, trange , arrow 0,0, 0,1,10,black arrow 0,0, 1,0 ,10,black vline 0,0, black hline 0,0, black linewidth 1 levelcurve blue, , linewidth 1 plot green,,
Masse et centre de masse
Calculez la masse et le centre de masse d'un fil fin qui suit la courbe
plane d'équations
,
,
[,]
si la densité
est donnée par
. Le calcul doit être fait avec une précision de
.
Masse et centre de masse 2
Calculez la masse et le centre de masse d'un fil fin qui suit la courbe
plane d'équation
pour
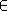
[
]
Masse et centre de masse 2 3D
Calculez la masse et le centre de masse d'un fil fin qui suit la courbe
de l'espace donnée par les équations
,
[,]
si la densité
est égale au carré de la distance
.
Masse et centre de masse 3D
Calculer la masse et le centre de masse d'un fil fin qui suit la courbe
de l'espace donnée par les équations
,
[,]
si la densité
du fil est donnée par
.
The most recent version
Cette page n'est pas dans son apparence habituelle parce que
WIMS n'a pas pu reconnaître votre navigateur web.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne
sont pas des fichiers
HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE.
Il est inutile pour vous de les ramasser par un programme robot.
- Description: collection d'exercices sur les intégrales curvilignes d'une fonction. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, analysis, line_integral, parametric_curves, length
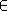 [,]
[,] 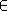 [,]
[,]  [
]
[
]