 内
.
计算
mod
.
内
.
计算
mod
. (出现的整数应该在 0 到 ) 之间. 你找到了 mod . 因此, 方程 mod 等价于
 /n
/n 里的计算的练习.
里的计算的练习.
约定 : 回答中的出现的整数应该在 0 和 之间.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里计算 / . 把结果表示成 0 到 的整数.
里计算 / . 把结果表示成 0 到 的整数.
 /
/ 里的零因子吗 ?
里的零因子吗 ?
 /
/ 里的零因子集. (这个练习的零因子不包括 0.)
里的零因子集. (这个练习的零因子不包括 0.) 把每个元素写成 1 到 之间的一个整数, 元素间用逗号分隔.
 /
/ 里有多少零因子 ?
里有多少零因子 ? 本练习中的零因子不包括 0.
 /
/ 内有两个根
与
.
计算之.
内有两个根
与
.
计算之. 设在  内
.
计算
mod
.
内
.
计算
mod
.
(出现的整数应该在 0 到
) 之间.
你找到了
mod
.
因此, 方程
mod
等价于
mod .
是否存在唯一的 0 与 之间的整数 同余于 mod 且使得
mod ?
回答 : 方程 mod 实际上等价于方程 mod .计算 0 与 之间的整数 , 它同余于 mod 且使得 mod . 方程 mod 有多少解 (模 ) 它同余于 mod ?
 /
/ 里求 的逆 . 把结果表示成 0 到 间的整数.
里求 的逆 . 把结果表示成 0 到 间的整数.
 /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
 /
/ 里求 的逆 . 把结果表示成 0 到 的整数.
里求 的逆 . 把结果表示成 0 到 的整数.
 /
/ ->
->  /
/ 它定义为 f(x)=x .
它定义为 f(x)=x . f 是双射吗 ?
 内方程
内方程
 mod
mod
解的集合
具有形式
 其中
是正整数,
是
其中
是正整数,
是 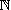 内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
内严格小于
的整数的有限集. 取
为其中最小者, 给出
内所有整数 .
解的集合
具有形式
 其中
是
内严格小于 的整数的有限集. 写出
的所有整数.
其中
是
内严格小于 的整数的有限集. 写出
的所有整数.
+


 /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 mod .
mod .
= =
 /
/ 内有元素 a , 使得 a 模 同余于 , 求 a.
内有元素 a , 使得 a 模 同余于 , 求 a. 把结果表示成 0 到 间的整数.
 1 mod .
1 mod .
计算最小整数 使得这个方程等价于
 1 mod
1 mod
计算最小整数 使得这个方程等价于
 1 mod .
1 mod .
 /
/ 内计算 . 把结果表示成 0 到 间的整数.
内计算 . 把结果表示成 0 到 间的整数.
 /
/ 内平方元的集合. (
内平方元的集合. ( /
/ 里的平方是可表成另一个元素平方的元素.)
里的平方是可表成另一个元素平方的元素.) 把每个元素表示成 0 到 间的整数, 元素间用逗号分隔.

 , 0
, 0 
 ,
, +  (mod ) , ×
(mod ) , ×  (mod ) .
(mod ) .
不考虑这两个数的次序.
 内的所有解
内的所有解 把解写成以下形式
| = * + * |
| = * + * |
 内.
内.
是否有模 的唯一解 ?
 内的所有解
内的所有解 把解写成以下形式
| = + * + * |
| = + * + * |
 内.
内.
请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地 使用. 您用自动化程序收集的网页是无用的.