Polynômes et séries formelles
Polynômes et séries formelles
I Séries formelles
Polynômes et séries formelles
→ I Séries formelles
I-1 L'anneau des séries formelles
I-2 Inversion, composition, dérivation
I-4 Récurrences linéaires à coefficients constants.
I-1 L'anneau des séries formelles
Polynômes et séries formelles
→
I Séries formelles
→ I-1 L'anneau des séries formelles
mais ces formules ne sont valables qu'à condition d'accepter la convention pour . En fait, les coefficients d'un polynôme ne sont pas les éléments d'une suite finie, mais ceux d'une suite infinie à support fini c'est-à-dire que l'on impose que les sont nuls, sauf pour un nombre fini de valeurs de . Si l'on s'affranchit de cette restriction, on arrive à un objet en un sens encore plus simple qu'un polynôme.
Dans la suite de ce chapitre, nous notons un anneau commutatif quelconque, mais nous sommes surtout intéressés par les cas , , ou .
Ë toute suite à valeurs dans un anneau commutatif , on associe donc une série entière formelle, notée
et on définit des opérations sur ces objets. Si est une autre série entière formelle, leur somme et leur produit sont définis par
Pour tout élément de la suite de coefficients et pour est associée à une série entière formelle que l'on note encore simplement . On dit que est une constante. On note l'ensemble des séries entières formelles à coefficients dans .
Théorème
Muni des lois ci-dessus, l'ensemble
des séries entières formelles à coefficients dans l'anneau commutatif
forme lui-même un anneau commutatif. Les éléments neutres de l'addition et de la multiplication sont les séries constantes
et
, et l'opposé de
est donné par
.
Démonstration
Il suffit de vérifier un à un les axiomes des anneaux commutatifs énoncés plus haut. Toutes ces vérifications sont immédiates. Nous traiterons seulement l'associativité de la multiplication et la distributivité. Soit donc
une troisième série. On a
et
Un anneau est intègre si l'équation dans implique ou .
Théorème
Si
est intègre,
l'est aussi.
Démonstration
Supposons
et
. La suite
n'est pas identiquement nulle. Il existe donc un entier
tel que
et
. De même, il existe
tel que
et
. Posons
. On a
puisque est intègre. On en déduit que le coefficent de dans est non nul et .
I-2 Inversion, composition, dérivation
Polynômes et séries formelles
→
I Séries formelles
→ I-2 Inversion, composition, dérivation
Proposition
Si
est une série entière formelle dont le coefficient constant est 1, il existe une unique série
telle que . Cette série sera notée .
Démonstration
La condition s'écrit
et
pour
. La suite définie par récurrence par
{ pour \( n\gt 0 \right.$ERROR} {array} .)
vérifie donc les hypothèses, et c'est la seule.Contrairement à ce qui se passe pour les polynômes, il n'est pas possible d'évaluer une série formelle en en un point . Par contre, il est possible de composer les séries et , ce qui revient à évaluer en , à condition que le coefficient constant de soit nul.
Proposition
Si
est une série entière formelle quelconque, et
est une série entière formelle dont le coefficient constant est nul,
il existe une série
et une seule, notée
ou
, telle que pour tout
soit le coefficient de
dans l'écriture de la série
pour tout
. On écrit aussi
.
On peut définir une dérivation. Si on appelle dérivée de et on note la série
On a les relations habituelles
Démonstration
Démontrons la deuxième égalité. On a
I-3 Quelques exemples
Polynômes et séries formelles
→
I Séries formelles
→ I-3 Quelques exemples
La série est inversible. Il est facile de voir que son inverse est
plus généralement, si , on peut écrire
On peut définir une exponentielle formelle dans
et un logarithme formel
et on a les relations
En effet, on voit facilement que et . On a donc , ce qui donne puisque le coefficient constant est 0. De même, , donc . Les coefficients de vérifient donc la récurrence , ou encore qui, compte tenu de , donne et pour , donc .
Pour tout et tout , introduisons la factorielle descendante définie par récurrence par et . Si et on peut définir
En effet, on a . Les coefficients de vérifient donc la récurrence , ou encore qui, compte tenu de , donne bien .
Si , la série est un polynôme, et on retrouve bien la formule du binôme. On a alors la
Proposition
Démonstration
En utilisant la formule du binôme, on prouve
et on obtient la relation cherchée en substituant
à
.
Explicitons en particulier le cas de la racine carrée
En effet, le coefficient peut s'écrire
en ``complétant la factorielle'' au numérateur par les facteurs impairs manquants , d'où le résultat.
I-4 Récurrences linéaires à coefficients constants.
Polynômes et séries formelles
→
I Séries formelles
→ I-4 Récurrences linéaires à coefficients constants.
Considérons par exemple la suite d'entiers définie par , et pour . On forme la série
en décomposant la fraction rationnelle en éléments simples, on obtient
et la formule finale .
Dans ce cas, le polynôme caractéristique avait deux racines distinctes, et . Voyons ce qui se passe s'il a une racine double. Définissons la suite par , et . Un calcul similaire donne
Cette dernière formule peut s'obtenir soit à partir de la formule générale pour avec , soit en remarquant que est la dérivée de .
I-5 Les nombres de Catalan
Polynômes et séries formelles
→
I Séries formelles
→ I-5 Les nombres de Catalan
Nous concluons cette section par un théorème célèbre dû à Euler (1707-1783). Nous allons calculer le nombre de chemins qui mènent du coin en bas à gauche d'un carré de côté au coin en haut à droite en suivant les côtés des carrés de côté 1, en allant toujours vers le haut ou vers la droite et sans jamais monter au dessus de la diagonale principale du carré. La figure ci-dessous illustre les chemins acceptables pour et prouve que . On voit facilement que et , mais comment obtenir une formule générale ?
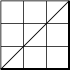

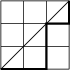


On voit que tout chemin acceptable commence par aller de à . Il refera contact avec la diagonale pour la première fois au point . L'entier est compris entre 1 et . Combien y a t'il de chemins acceptables pour une valeur donnée de ? Juste avant d'atteindre , le chemin venait forcément de et entre les points et , il parcourt un chemin acceptable dans le carré de sommets et qui est de côté . La figure représente un cas avec et .
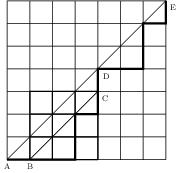
qui permet de calculer les par récurrence. On a donc , , etc. Formons la série génératrice . On a donc
en posant . On reconnait sur la droite le développement de . On a donc prouvé
ce qui est une équation du second degré en . La résolution habituelle de l'équation , de discriminant donnerait
Le choix du signe ne donne pas une série entière formelle. En utilisant la formule ci dessus pour , on trouve
On a donc
et la formule
On pourrait objecter que la formule pour la résolution des équations du second degré n'a pas été démontrée dans le cadre des séries entières formelles. Pour compléter le raisonnement, on peut partir de la solution proposée: la série
vérifie bien . En soustrayant cette équation à , on trouve . Comme le facteur n'est pas nul et est intègre, on en déduit bien .
Les nombres de Catalan ne comptent pas seulement des trajets dans un carré. On peut montrer que est le nombre de façons de diviser en triangles un polygone convexe à côtés, le nombre de façons correctes d'imbriquer parenthèses ouvrantes et parenthèses fermantes, le nombre d'arbres binaires pleins à noeuds intérieurs, etc.
II Polynômes
Polynômes et séries formelles
→ II Polynômes
II-1 Relations entre racines et coefficients
II-1 Relations entre racines et coefficients
Polynômes et séries formelles
→
II Polynômes
→ II-1 Relations entre racines et coefficients
On peut encore utiliser la formule du produit en posant et . On trouve
ce qui suggère de regrouper les de même cardinal :
où
est le -ième polynôme symétrique élémentaire des . Par exemple, pour , en notant , , et plutôt que , , , , on trouve
II-2 Polynômes symétriques
Polynômes et séries formelles
→
II Polynômes
→ II-2 Polynômes symétriques
Un polynôme de plusieurs variables est dit symétrique s'il ne dépend pas de l'ordre des variables. Par exemple chaque est une fonction symétrique des . En fait tous les polynômes symétriques s'obtiennent à partir de ces derniers, ce qui justifie leur nom.
Théorème
Pour tout polynôme
symétrique en les indéterminées
, il existe un polynôme
(et un seul) tel que
.
Démonstration
Nous allons prouver l'existence de en énonçant un algorithme permettant de le calculer. On peut ordonner les monômes de la façon suivante: vient avant si et seulement si , ou et , ou et et , etc. Tout polynôme non nul a un terme dominant qui est le premier qui intervient avec un coefficient non nul. Si est symétrique, on voit que ce terme vérifie . On définit alors
Substituons à , puis développons en les . On obtient un polynôme symétrique en les et un examen attentif montre que le terme dominant du polynôme est le même que celui de . Cela justifie l'algorithme suivant
Donnée: un polynôme f symétrique en n indéterminées Sortie: un polynôme g satisfaisant à la condition du théorème
g <- 0 tant que f n'est pas nul faire g <- g + s(f) f <- f - t(f) fin tant que
Il reste à voir que l'algorithme s'arrête. Cela est dû au fait que la suite des termes dominants est strictement décroissante au sens de l'ordre défini plus haut et que cet ordre lexicographique est un bon ordre dans lequel, comme dans , toute suite strictement décroissante est finie.
Donnons un exemple du procédé. Nous prenons et les variables , et plutôt que , et . On part du polynôme symétrique
présenté en ordre lexicographique décroissant. On a donc et , donc
On recommence donc avec une nouvelle valeur de
Le terme dominant est et , donc
On recommence donc avec une nouvelle valeur de
Le terme dominant est et donc
ce qui achève l'algorithme. Le polynôme obtenu est donc et on obtient l'identité
II-3 Les formules de Newton
Polynômes et séries formelles
→
II Polynômes
→ II-3 Les formules de Newton
Nous allons donner une version explicite du théorème précédent dans un cas particulier. Notons
la somme des puissances -ièmes des . C'est une fonction symétrique des , que l'on peut donc exprimer en fonction des . Il est en fait possible de calculer les par récurrence grâce aux formules de Newton:
Théorème
Pour
, on a
et pour
Démonstration
Partons de la relation de définition
Le coefficient de dans le premier membre est
dérivons-la
divisons membre à membre ces deux égalités
substituons à et chassons les dénominateurs en
Écrivons le développement en série formelle du premier membre:
L'identité ci-dessus peut donc s'écrire
ou encore
Le coefficient de dans le premier membre est
La comparaison avec le second membre donne les formules de Newton.
On déduit de ces formules l'expression des en fonction polynômiale des :
II-4 Un exemple
Polynômes et séries formelles
→
II Polynômes
→ II-4 Un exemple
On en déduit les sommes de puissances successives
et ainsi de suite. On remarque que cette procédure est en quelque sorte l'inverse de celle concernant les récurrences linéaires à coefficients constants: au lieu de partir d'une suite qui satisfait une récurrence linéaire et de trouver des qui permettent d'exprimer comme combinaison linéaire des puissances -ièmes des , on part des et on trouve une récurrence linéaire satisfaite par la suite .