Fonctions, Applications
Sommaire
Ce document est une introduction à la théorie des fonctions. Il fait suite au Doc Ensembles . Nous revenons aussi sur les propriétés des applications. Le DOC Raisonnements est utile à la lecture de certaines parties de ce cours.
- Généralités
- Image, composition de fonctions
- Injection, surjection, bijection
- Propriétés graphiques
- Bibliographie
Fonction (définitions)
On appelle fonction la donnée d'un ensemble , d’un ensemble et d’un « procédé » qui permet d’associer à un élément de E au plus un élément de F. Cet élément , quand il existe, est l’image de , et est appelé un antécédent de .
On appelle l'ensemble de départ de , l'ensemble d'arrivée de .
L'ensemble de définition d'une fonction , noté souvent , est la partie de l'ensemble de départ dont les éléments admettent des images par .
Dans les pages suivantes, on explicite différentes façons de définir une fonction.
- Par un tableau
- Par un diagramme sagittal
- Par une représentation graphique , fournie sans formule de calcul. (Statistique, relevé météo, diagramme, etc...)
- Par une formule explicite
Tableau, Diagramme sagittal
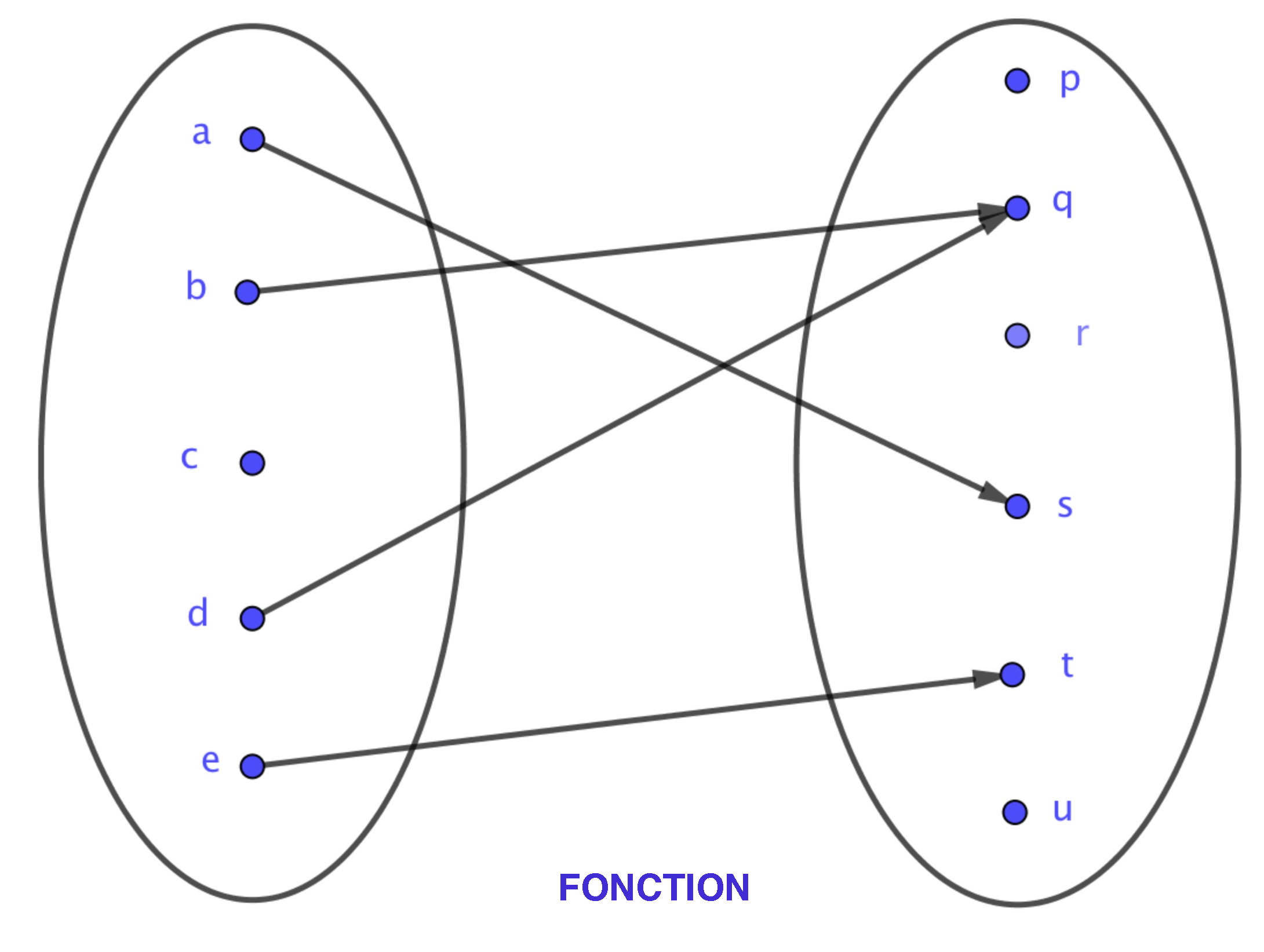
Diagramme sagittal
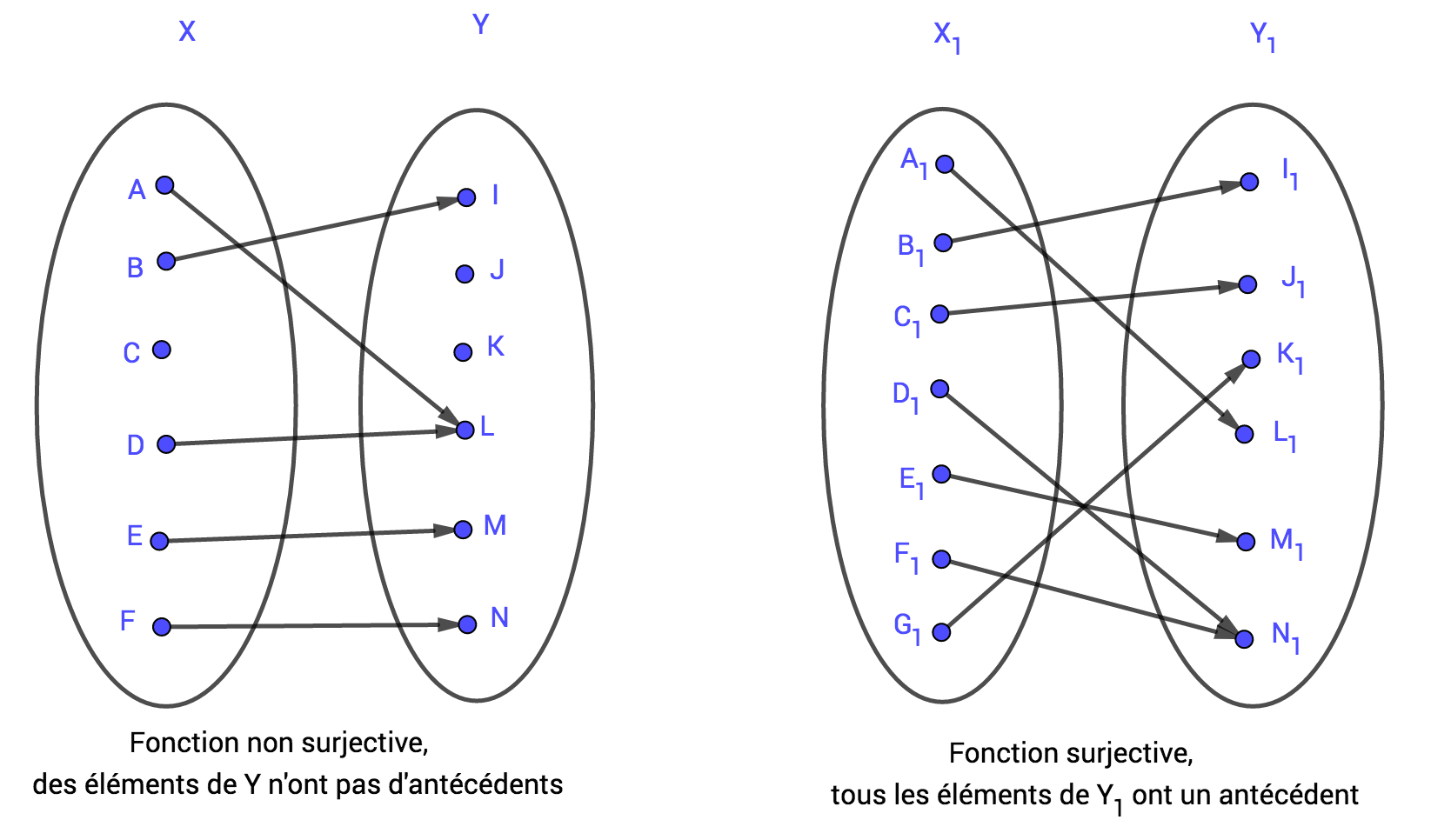
Pour des ensembles finis, on peut dessiner deux "patates" représentant les ensembles et , et, lorsqu'un élément de est l'image d'un élément de , tracer une flèche de cet élément de vers l'élément de . Plus élégamment, on parle de diagramme sagittal.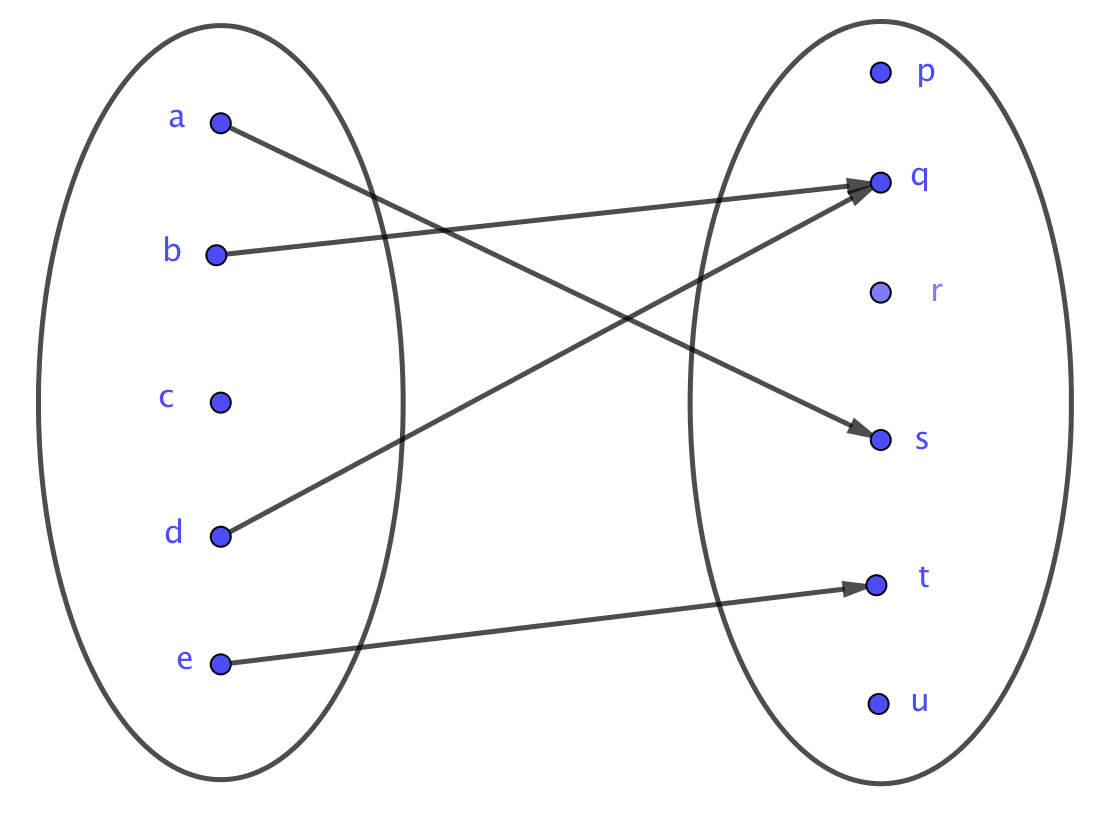
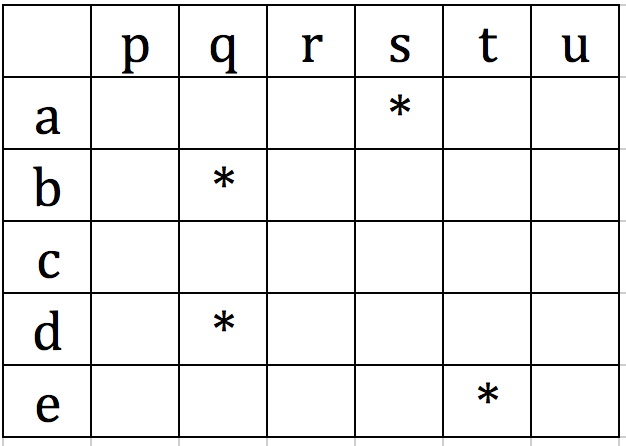
Tableau
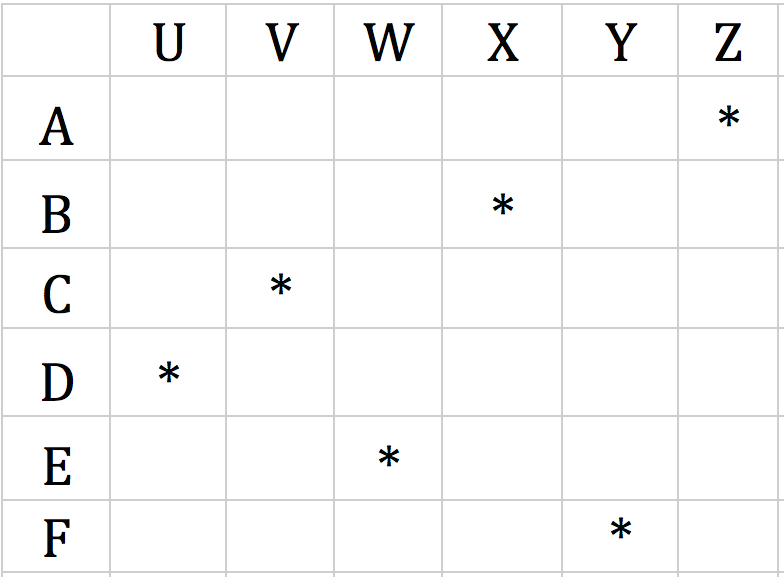
Toujours pour des ensembles finis, on peut définir une fonction par un tableau avec les éléments de dans la première colonne, ceux de dans la première ligne en mettant une croix ou un signe dans le tableau, à l'intersection d'une ligne et d'une colonne, lorsque deux éléments de et de sont en relation par .Le tableau ci-dessous représente une fonction de vers . Ainsi a pour image par (ce que l'on a matérialisé par une étoile ici), a pour image , etc..., et n'a pas d'image.
Représentation graphique
- Le graphe d'une fonction de E dans F, est la partie de définie par
- La représentation graphique d'une fonction de dans est l'ensemble des points du plan dont les coordonnées appartiennent à , graphe de .
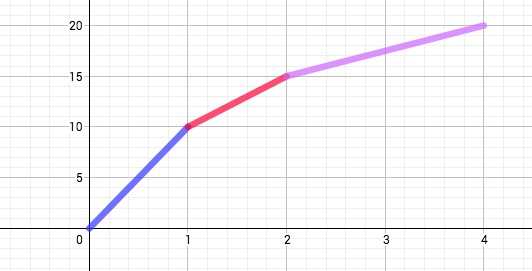
Un cycliste roule pendant une heure à 10 km/h, puis à 5 km/h l'heure suivante et enfin à 2,5 km/h les deux heures suivantes. La fonction qui associe au temps la distance parcourue est donnée par la représentation graphique suivante ; l'axe des abscisses est gradué en heure et l'axe des ordonnées en kilomètres.
Fonction définie par des formules
Fonction numérique de variable réelle
On peut définir une fonction numérique de dans en donnant pour la variable réelle une formule pour calculer le réel .
pour
.
Que valent
?
; n'est pas défini.
Cette fonction admet la représentation graphique suivante :
À partir de la représentation graphique d'une fonction, on peut retrouver les formules la définissant.
On donne la représentation suivante définissant l'évolution d'un phénomène.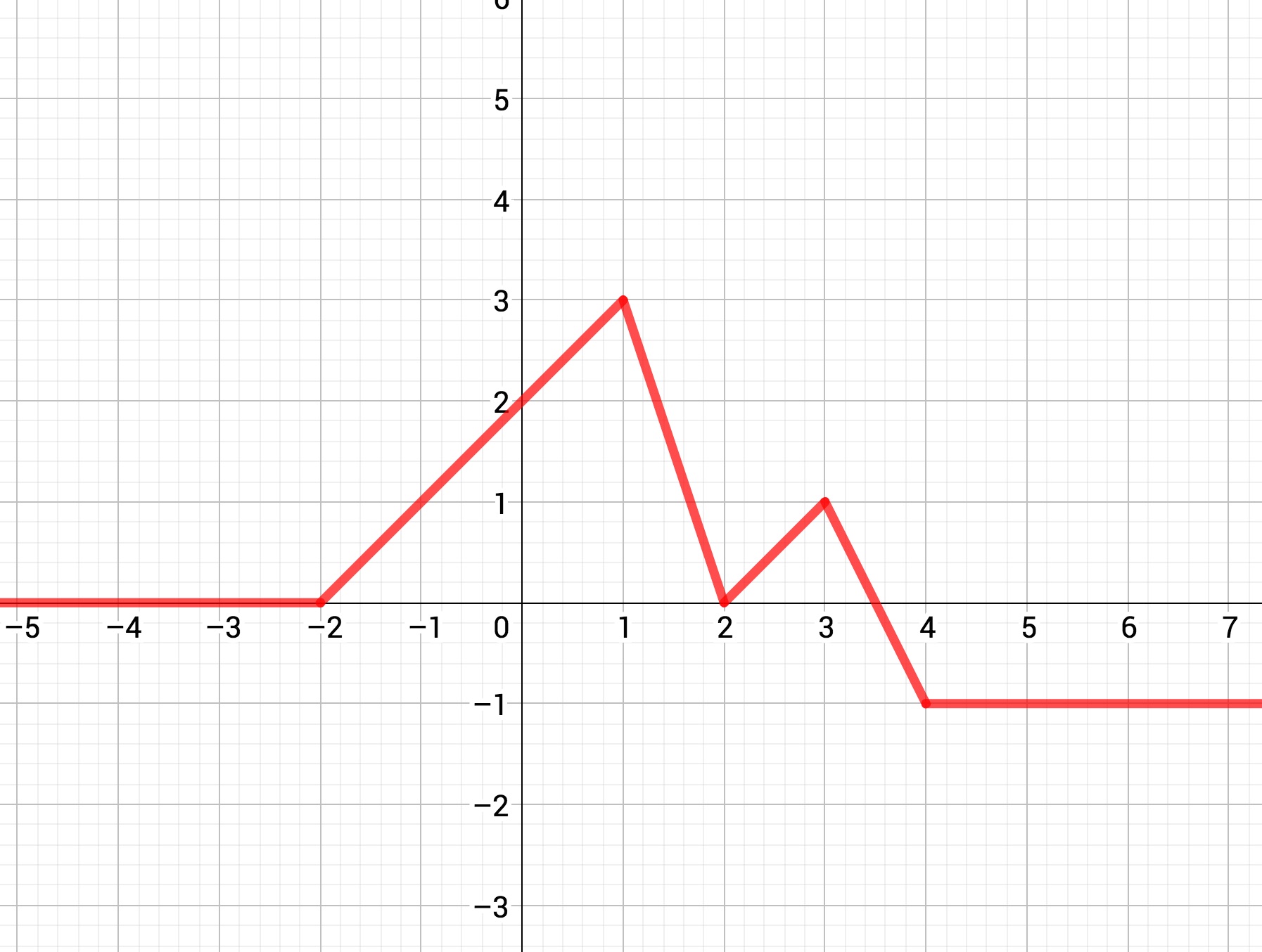
On rappelle que l'équation de la droite passant par les deux points et est : .
pour
pour
pour
pour
pour
pour
Applications
- La différence entre fonction et application ne concerne donc que l'ensemble de départ.
- On transforme facilement une fonction en une application en prenant son ensemble de définition pour ensemble de départ.
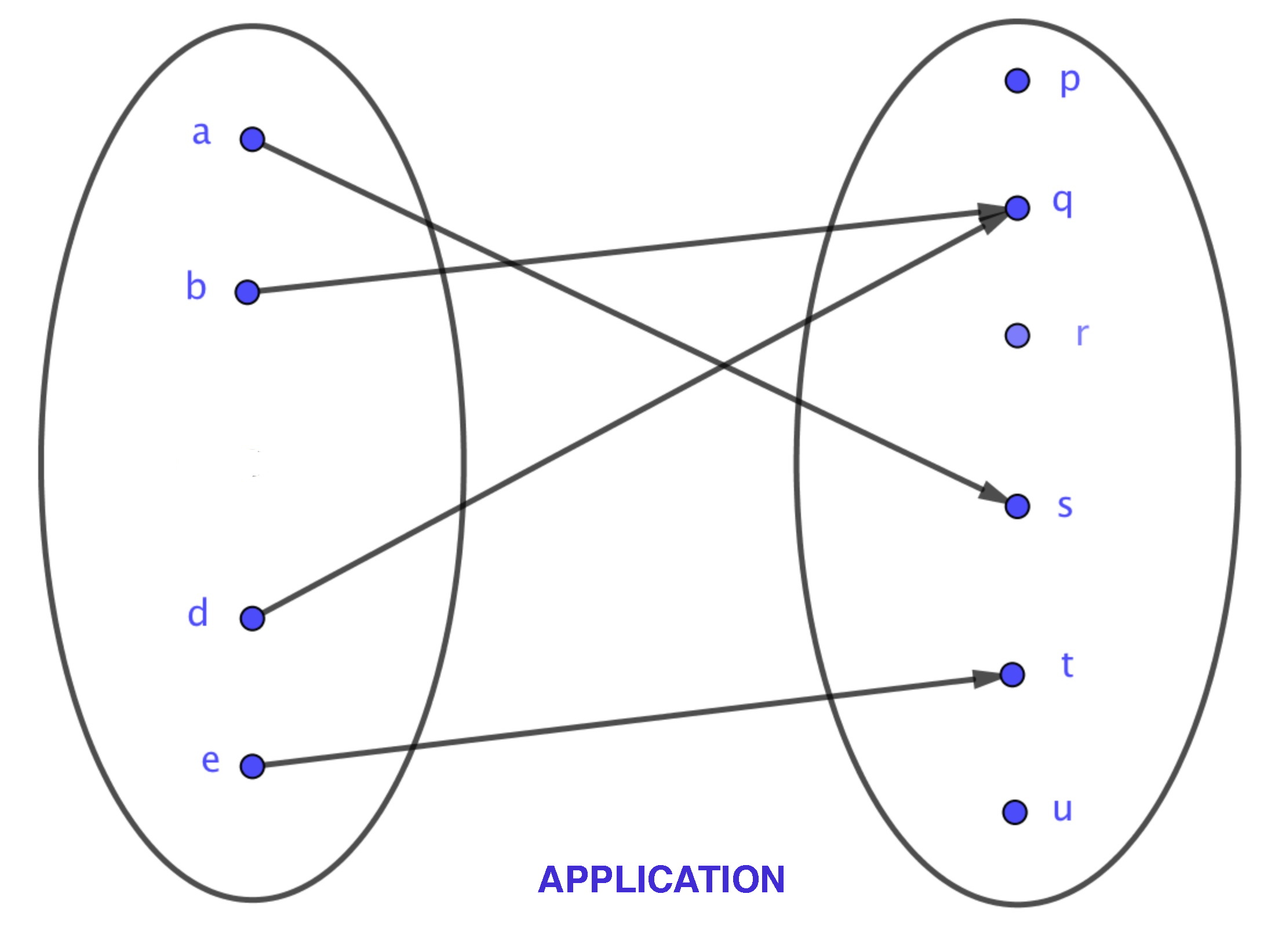
Dans l'exemple défini par Tableau, Diagramme sagittal , la fonction de vers devient une application si l'on prend pour ensemble de départ ( son ensemble de définition).
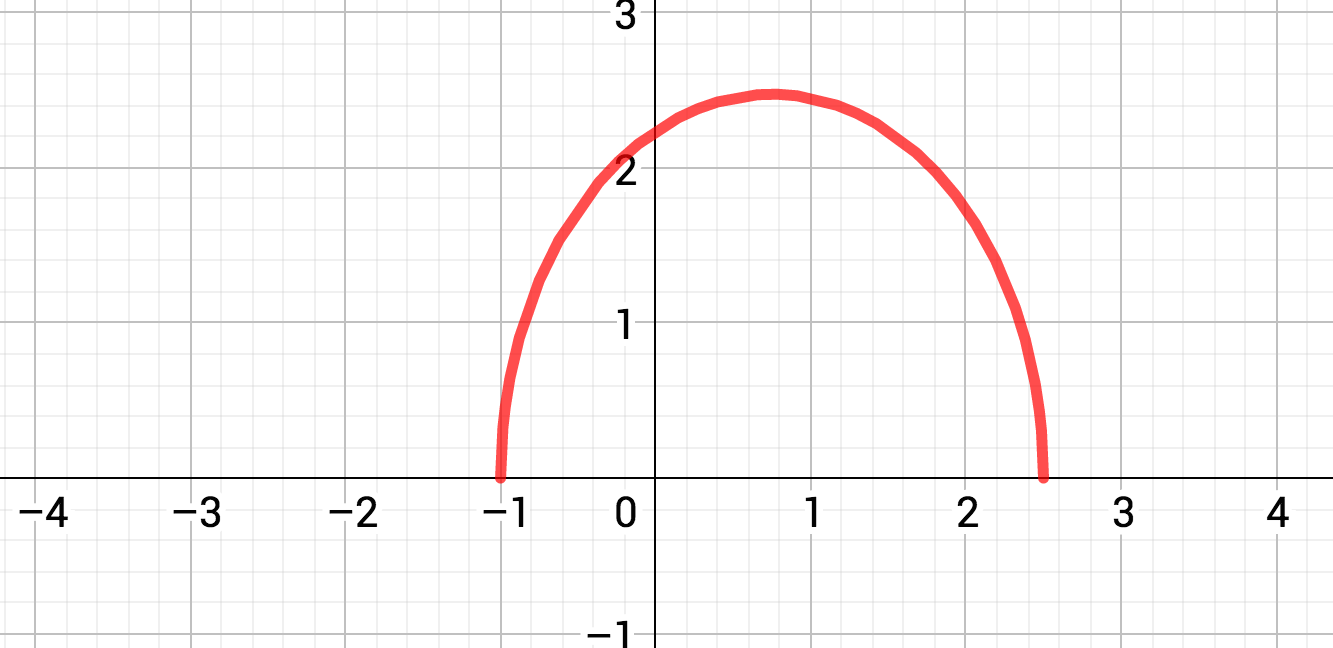
On considère la fonction de
dans
, définie par
.
Comment modifier l'ensemble de départ de la fonction
pour la transformer en une application ?
Tracer sa représentation graphique sur ce nouveau domaine de définition, dans un repère orthonormé.
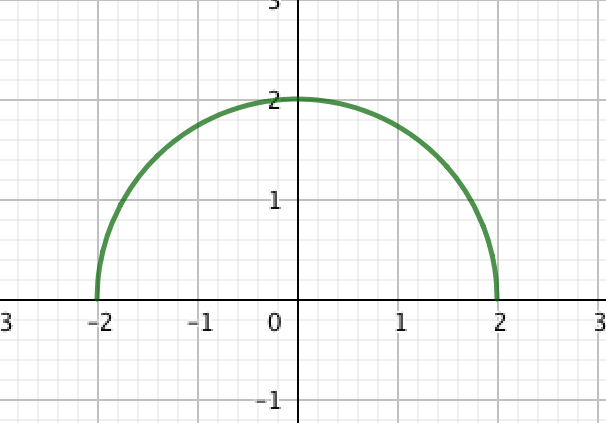
Si on remplace l'ensemble de départ de la fonction par son domaine de définition [], devient une application.
Les coordonnées des points de la représentation graphique vérifient l'égalité , équivalente à et . On reconnaît l'équation du demi-cercle de centre de rayon , dans le demi plan . Voici la représentation graphique de :
Sur le dessin ci-dessous, le point est l'image du point par la symétrie centrale de centre , et le F vert est l'image du F bleu.Vous pouvez déplacer tous les objets rouges.
Rappel : Définition et propriétés d'une symétrie centrale
Diagramme sagittal d'une application
Restriction d'une fonction.
- Pour transformer une fonction de vers en une application, on prendra sa restriction, notée par exemple, à l'ensemble de définition de . Si est une fonction de vers , est une application de vers .
- On notera bien que et ne sont pas les mêmes objets mathématiques (bien que l'écriture soit la même) puisque leurs ensembles de départ sont différents.
- On a souvent besoin de ne conserver de l'ensemble de définition d'une fonction qu'une partie où elle est strictement monotone (voir Théorèmes sur la bijection ). On prendra donc sa restriction à une partie judicieusement choisie. Par exemple, pour la fonction définie sur par , on prendra sa restriction à où elle est strictement croissante. (On pourrait prendre, de la même manière, sa restriction à , où elle est strictement décroissante).
- Dans GeoGebra, la syntaxe pour afficher la restriction, à l'intervalle [
] par exemple, de la fonction,
définie sur
par
, est
ou Si
On a tracé ci-dessous les courbes représentatives de la fonction définie a priori sur par (en violet), puis celles de ses restrictions et , respectivement aux intervalles [ ] (en bleu), puis [ ] (en marron).
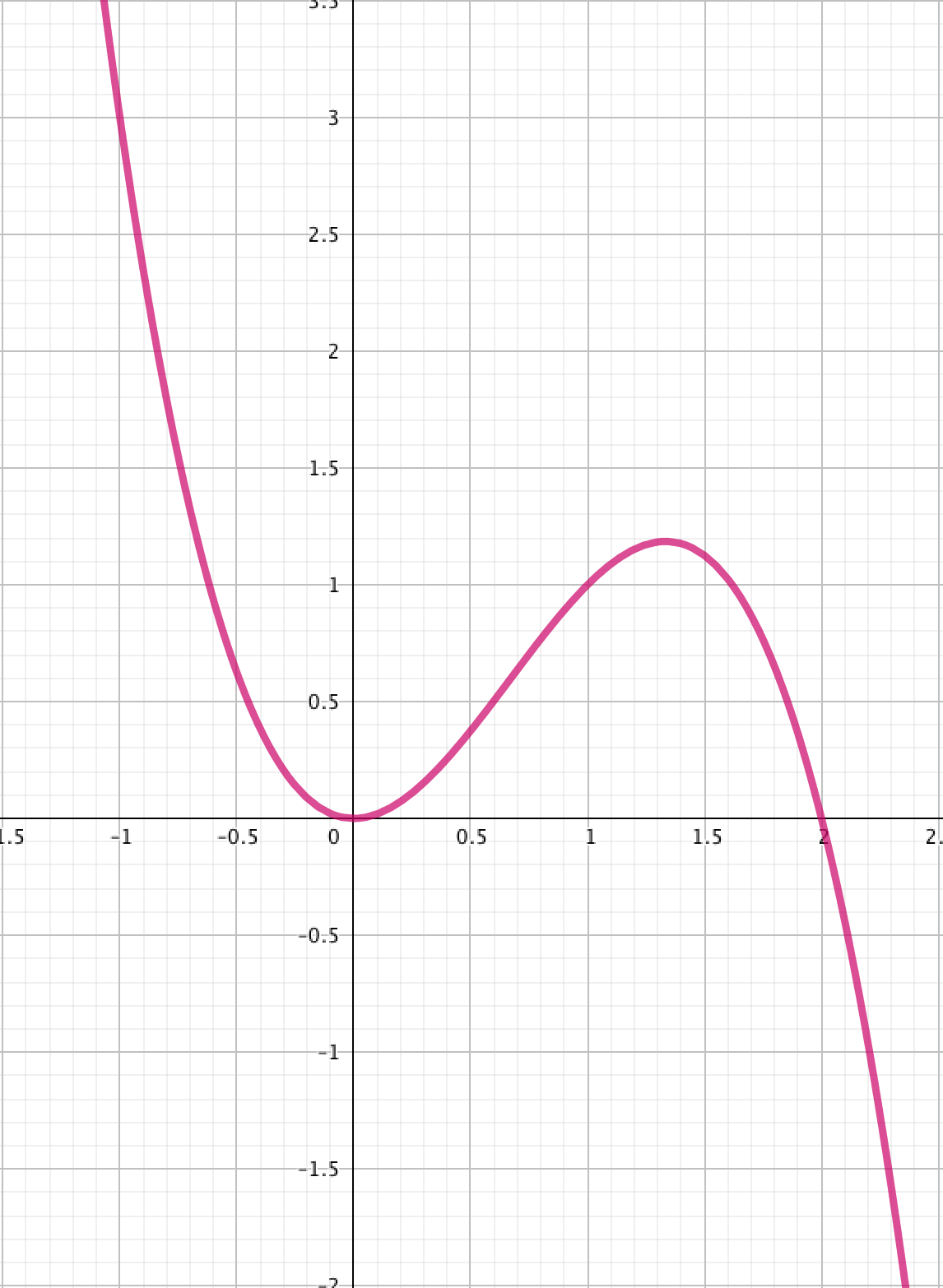
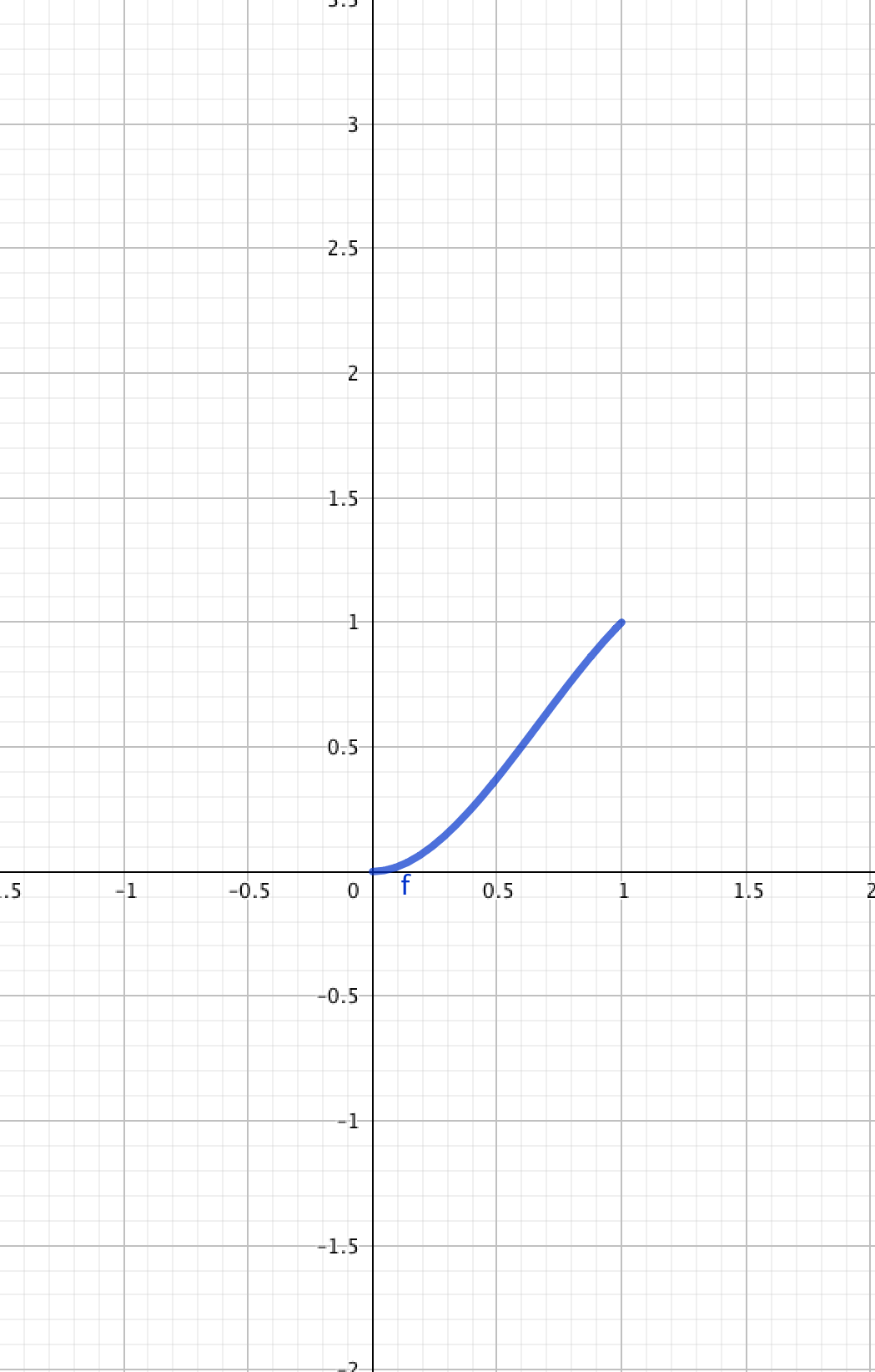
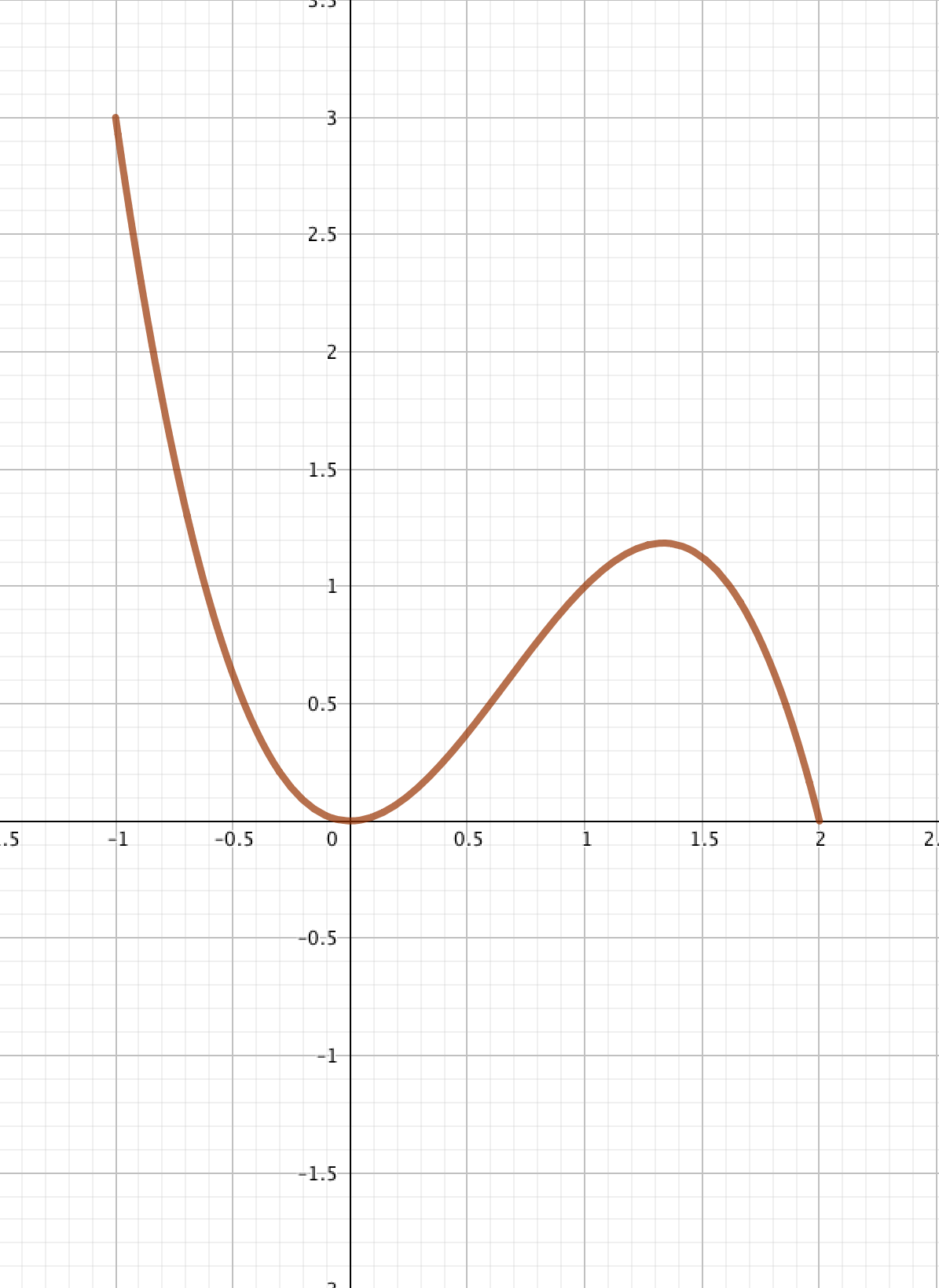
Image d'une fonction
Remarque. On veillera à ne pas confondre deux choses portant un peu le même nom :
- l’élément y, image de l’élément par la fonction , c'est-à-dire ; l’élément est un élément de
- La partie de l'ensemble d'arrivée de la fonction appelée image de la fonction . C'est un ensemble, une partie de .
Illustrations graphiques. Dans les deux figures ci-dessous, on a indiqué en rouge les images de deux fonctions, l'une donnée par son diagramme sagittal, l'autre définie sur par par sa représentation graphique.
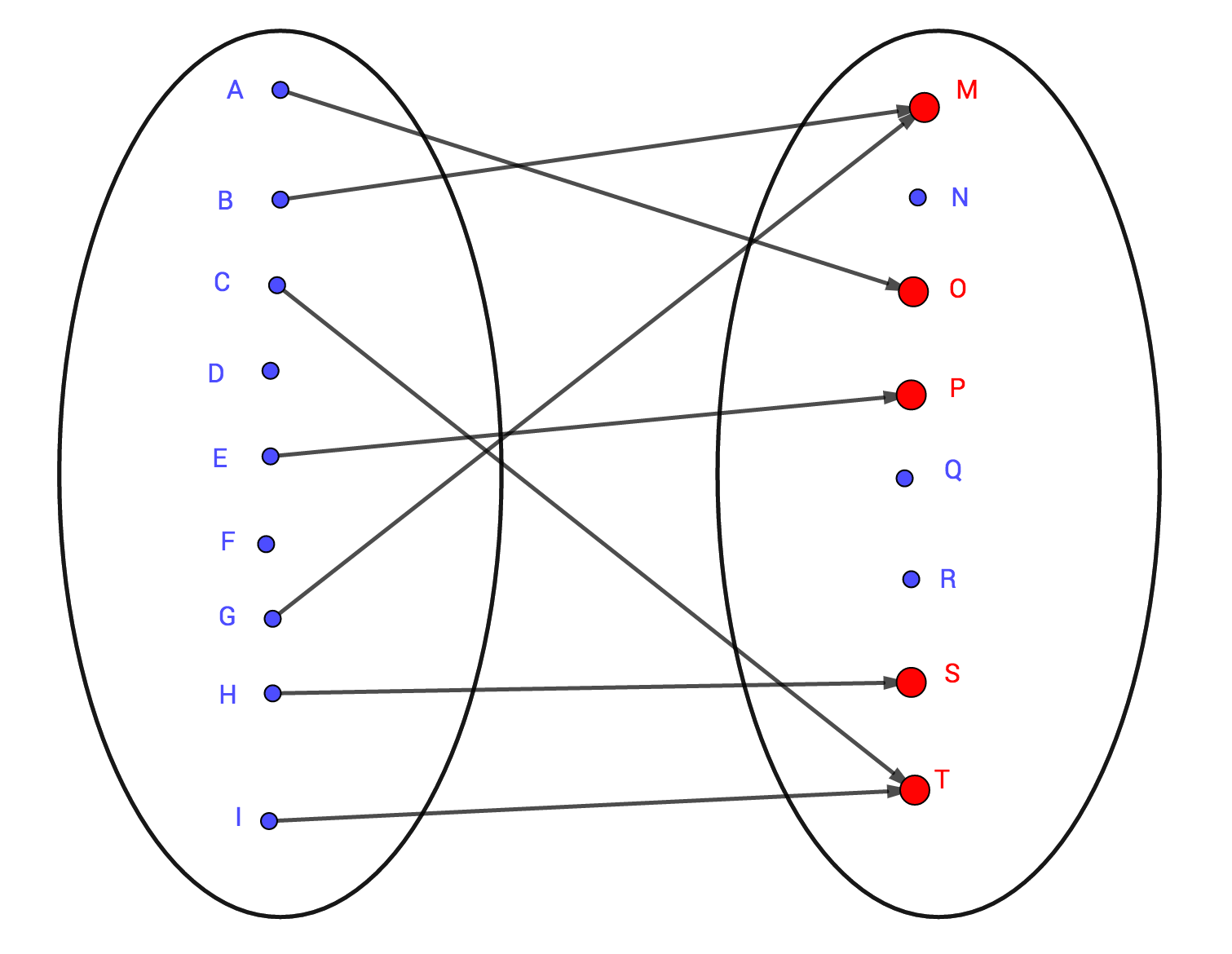 |
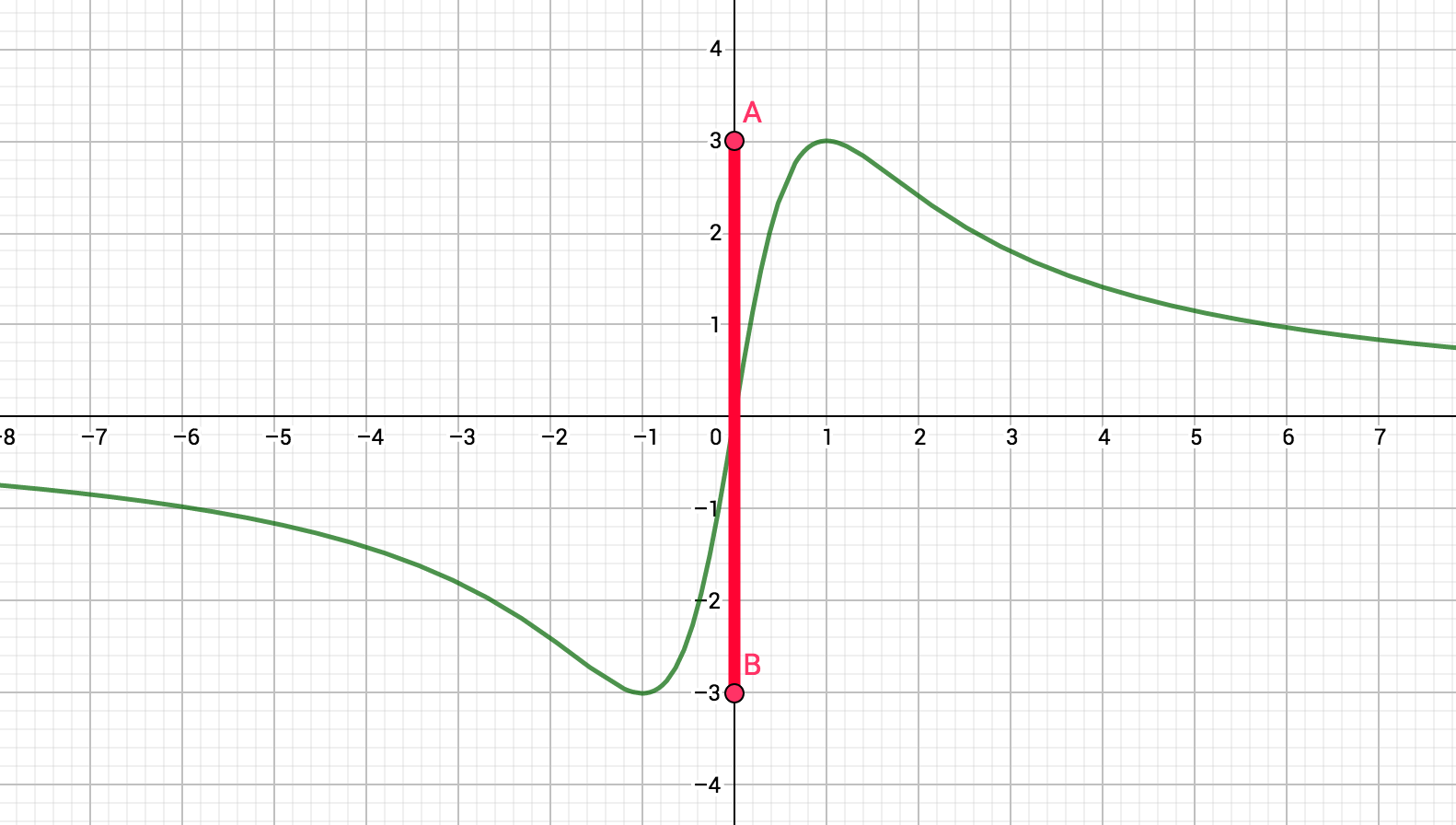 |
- Dans l'exemple de la page Tableau, Diagramme sagittal ,
- , définie par: . .
- , définie par: . Le minimum de la fonction est obtenu pour . L'ordonnée du minimum est d'où
- Pour
:
,
, on a
.
Choisissons , a priori quelconque, dans l'ensemble d'arrivée et cherchons ses antécédents, s'il en a. Ce sont des couples solutions de l'équation à deux inconnues et : .
- Choisissons pour une valeur fixée quelconque dans . En remplaçant dans l'équation, on obtient pour une valeur : . Le couple est donc une solution de l'équation et un antécédent de , quel que soit .
- On peut aussi choisir d'abord arbitrairement dans .
- Cas : on peut prendre dans l'équation de départ et quelconque dans .
- Cas : l'équation conduit à .
On peut donc prendre quelconque dans et .
En définitive on obtient
- Image d'une application donnée par un tableau . On rappelle que le cardinal d'un ensemble fini est son nombre d'éléments distincts.
- Image par un polynôme
- Pour les fonctions suivantes, de
dans
, déterminer
.
- Solution : ,
- Soit
l'application de
dans
, définie par
.
Quelles sont les images des couples et ? a-t-il des antécédents?
Les images : , .
Le nombre -5 a pour antécédents les couples tels que . En choisissant arbitrairement par exemple avec , on en déduit . Comme pour tout dans , le nombre est aussi dans , l'ensemble des antécédents de est : S = { }
Image réciproque d'un ensemble par une fonction
Soient une application de dans et une partie de , on appelle image réciproque de , notée , la partie de définie par : .
Autrement dit, l'image réciproque de est l'ensemble des antécédents des éléments de .
- Dans l'exemple du tableau et du diagramme sagittal, on a : , , ,
-
, définie par:
, (
).
- Pour déterminer , on résout dans l'équation . On obtient deux solutions : et . Donc on a : .
- Déterminer . La fonction s'annule pour et et est du signe du coefficient de (positif) à l'extérieur des racines ( théorème sur le signe du trinôme ), donc on obtient : .
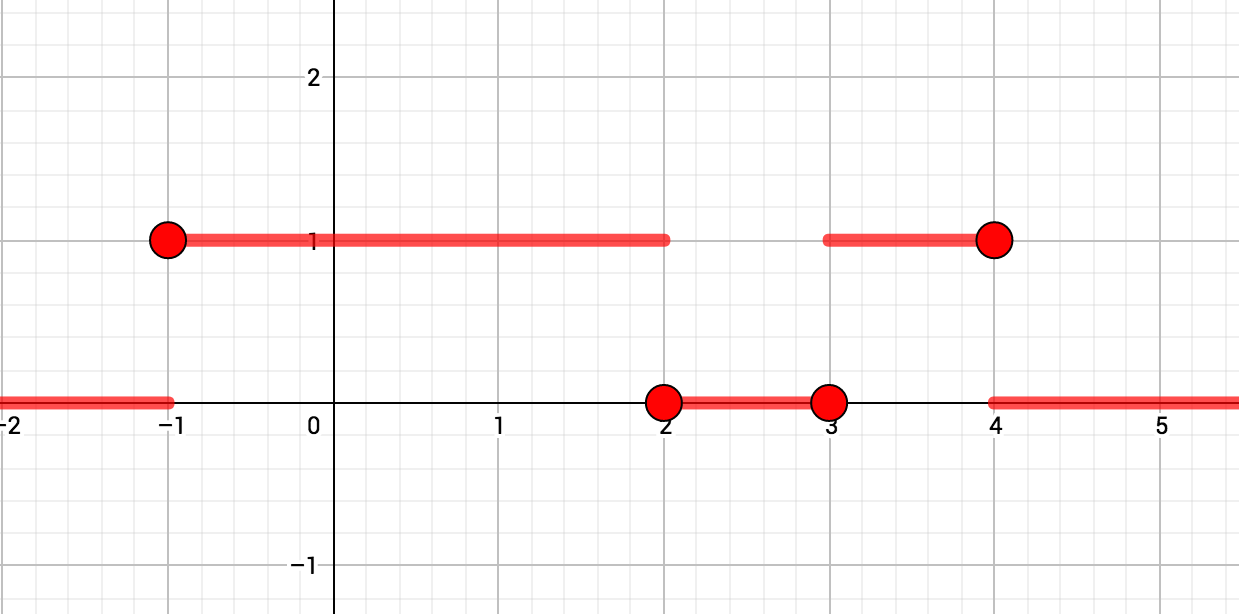
- Considérons la restriction à l'intervalle
de la fonction
définie sur
par
.
On pose :
et
.
L'image réciproque du segment de l'axe est la réunion des trois segments rouges :
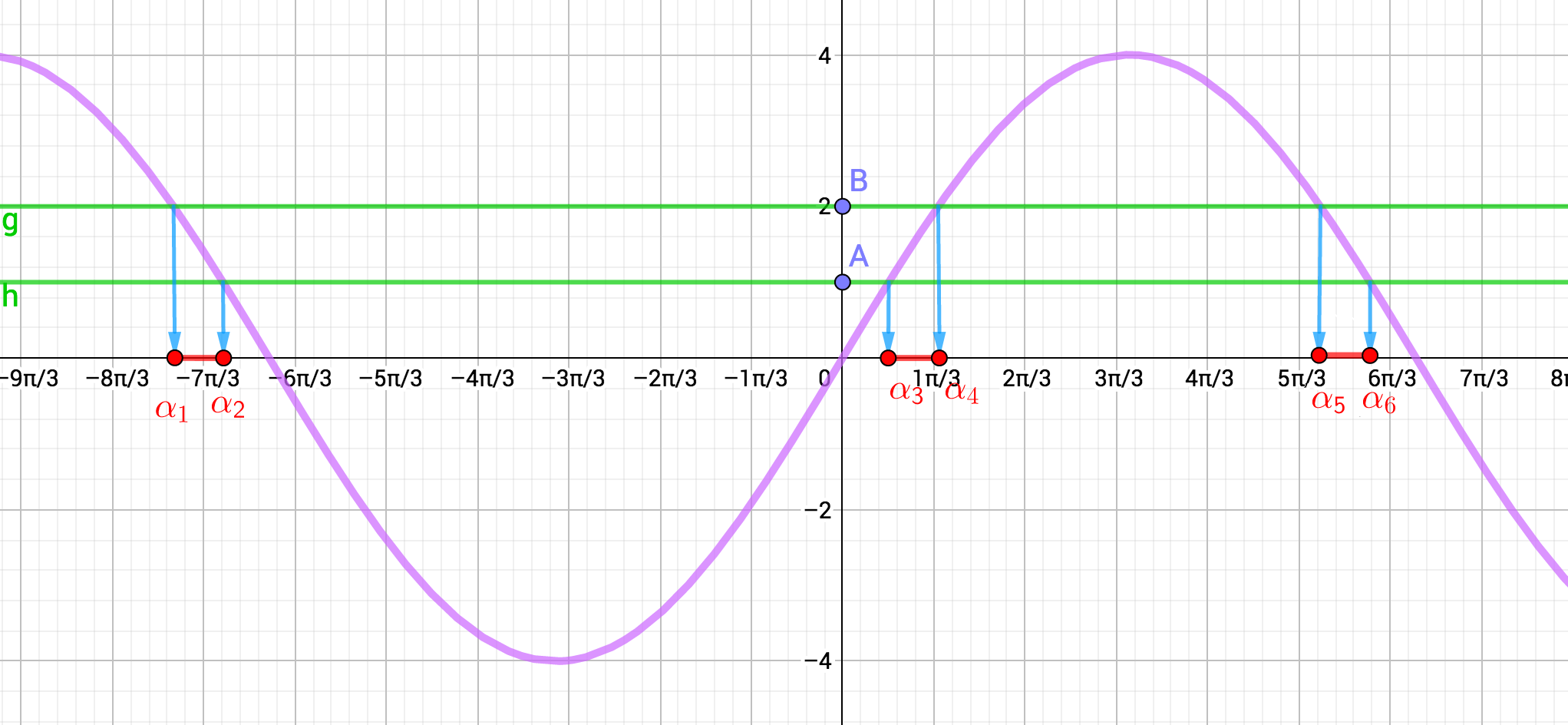
- Pour les fonctions suivantes, de
dans
, déterminer
.
- (On discutera suivant les valeurs de )
-
Image réciproque d'un intervalle
Aide
- Comparer \(f(f^{-1}(I))\) et \(I\) , étant un intervalle.
- Comparer \(f^{-1}(f(I)) \) et \(I\) , étant un intervalle.
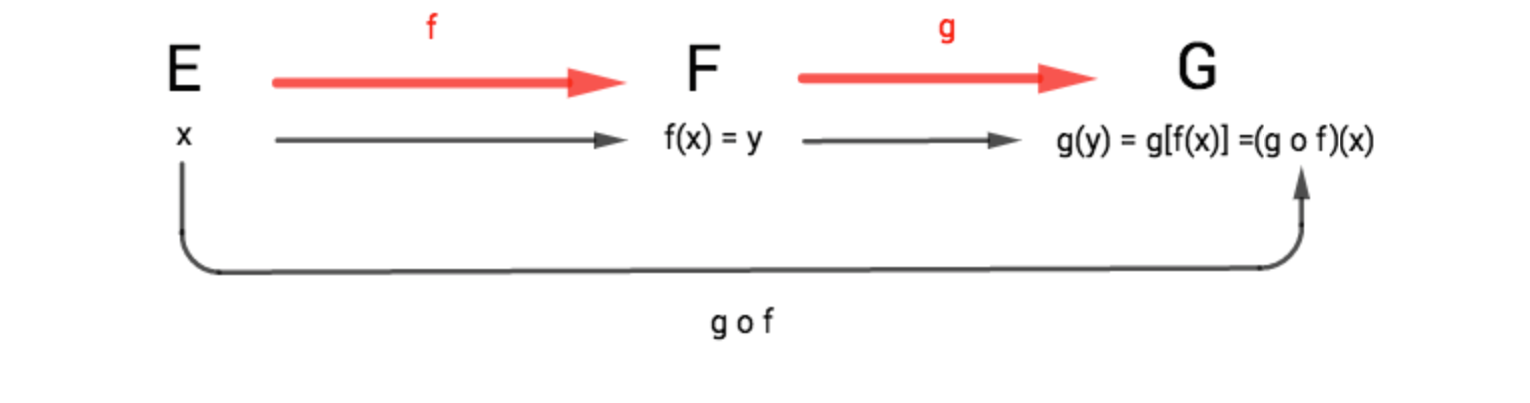
Composée de fonctions
Soient , et trois ensembles, une fonction de dans et une fonction de dans , suivie de . On appelle composée des fonctions et , notée (lire " rond "), la fonction de dans , définie pour et , par
- Exemples graphiques de composition
- Soient
et
les applications de
dans
définies par
et
.
La composé de
et
, ainsi que celle de
et
, sont possibles.
- est définie sur par .
- est définie sur par .
- Soit
l'application de
dans
, définie par :
et
l'application de
dans
, définie par :
.
- De l'équivalence , on déduit que l'ensemble de définition de est alors est l'application de dans , définie par : .
- est l'application de dans , définie par : .
- Soit
l'application de
dans
, définie par :
et
l'application de
dans
, définie par :
.
- est l'application de dans , définie par :
- n'est pas définie, car l'ensemble d'arrivée de la première application est = ] , -1], lequel n'est pas inclus dans l'ensemble de définition de qui est .
- Décomposition sous diverses formes
Remarque. On ne peut pas toujours composer des fonctions. Considérons la fonction de dans , définie par et la fonction définie par . L'ensemble d’arrivée de est , l'ensemble de départ de est . On ne peut pas composer et .
- Calcul d'image par \(g \circ f\)
- Composition et enchainement
- Composition et ensemble de définition
Exemples graphiques de composition
Soient trois ensembles , et . On considère une fonction de dans et une fonction de dans représentées par leurs diagrammes sagittaux ci-dessous.
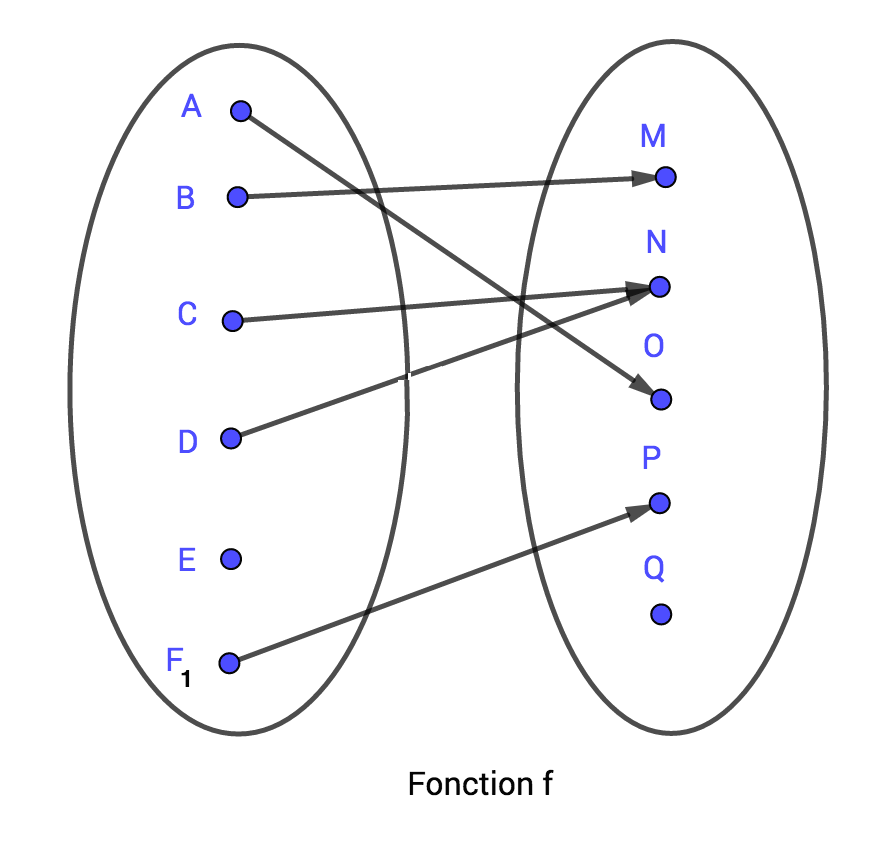 |
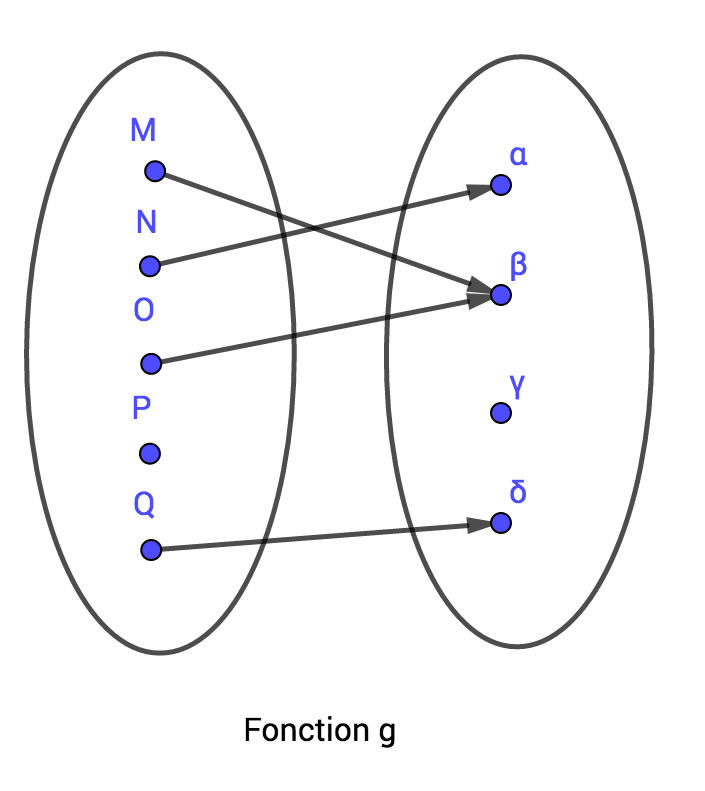 |
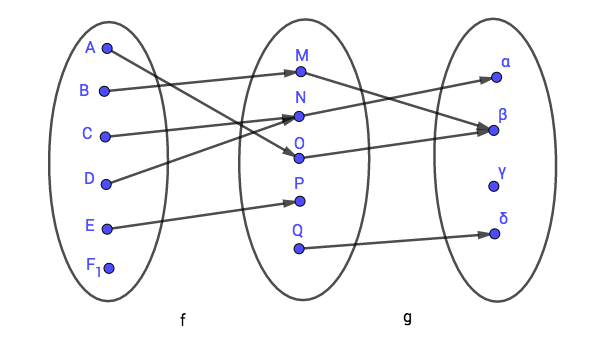 |
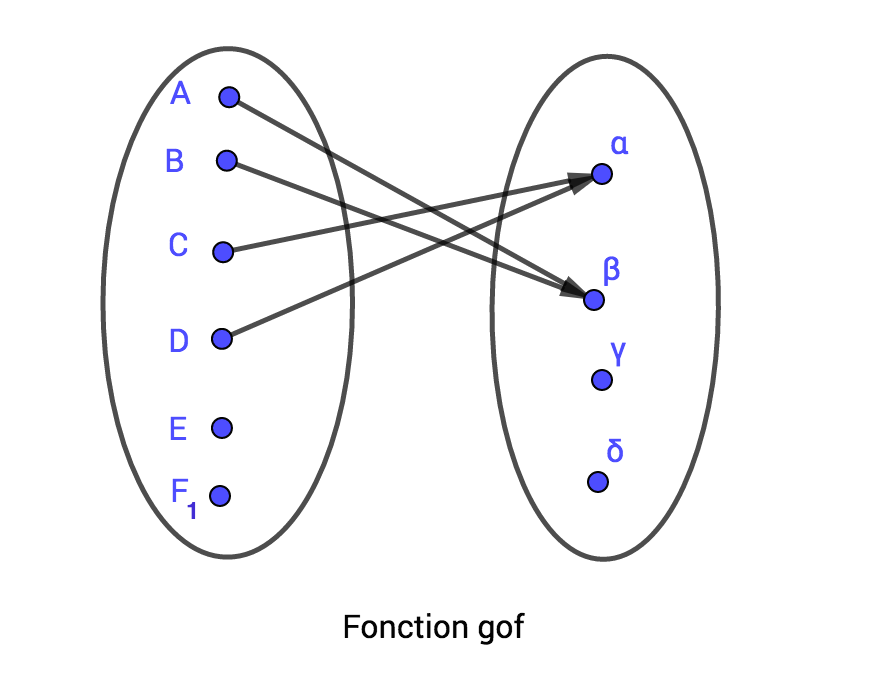 |
Injection
- On dit que une application ou une fonction de dans est injective ou une injection si tout élément de admet au plus un antécédent dans .
- On peut aussi formuler cela de la façon suivante : deux éléments distincts de l'ensemble de départ ont des images distinctes par dans l'ensemble d'arrivée , ce qui s'écrit avec des quantificateurs :
- Dans le cas d'un diagramme sagittal, une fonction n'est pas injective si deux flèches arrivent sur le même élément de l'ensemble d'arrivée. Lorsqu'on a fait un tableau, la fonction n'est pas injective lorsqu'il y a deux étoiles dans la même colonne. C'est le cas dans cet exemple .
- En prenant le restriction d'une fonction
à une partie de son ensemble de départ, on peut rendre celle-ci injective, si elle ne l'est pas.
Ainsi en tant que fonction de dans , définie par n'est pas injective, mais sa restriction à l'est.
L'injectivité d'une fonction dépend essentiellement de son ensemble de départ. - Soit une application de dans . Si et sont deux ensembles finis et qu'on ait , alors l'application n'est pas injective.
- Dans le cas d'une fonction donnée par une formule, on résout dans
, pour un
quelconque dans
, l'équation d'inconnue
:
.
Si, pour tout dans , elle admet au plus une solution dans , alors est une injection de dans . - Graphiquement, une fonction est injective si et seulement si toute droite horizontale coupe la courbe représentative
de cette fonction en au plus un point.
Dans l'exemple et le dessin ci-dessous, la courbe verte, courbe représentative d'une fonction , est coupée en quatre points , , et par la droite d'équation , la fonction n'est donc pas injective sur la partie de l'axe du dessin. Les antécédents de sont les abscisses des quatre points , , et .
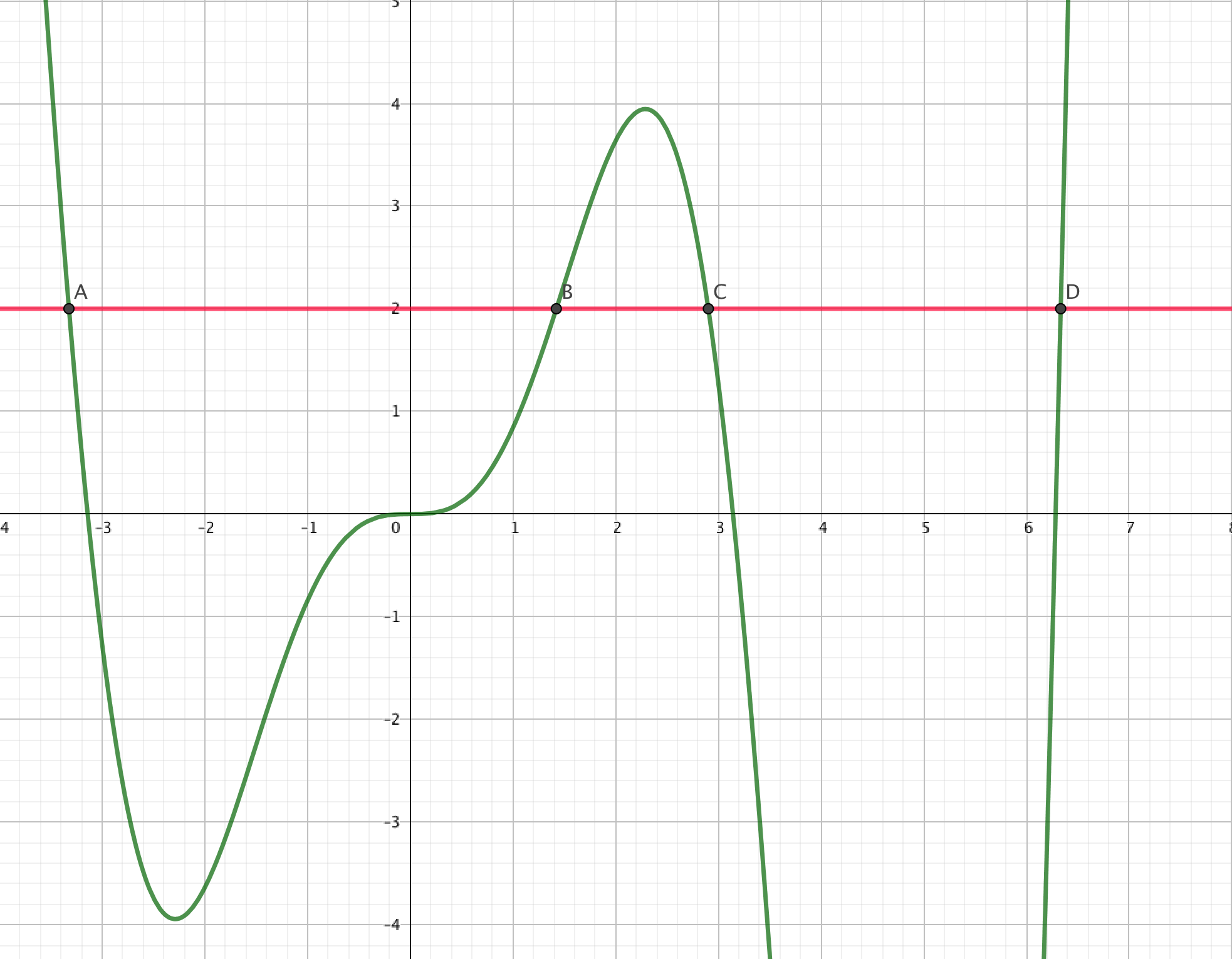
Injection, exemples, exercices
Première méthode. Soit , résolvons l'équation (d'inconnue ) : . On trouve une (unique) solution . La fonction de dans est donc injective.
Deuxième méthode. s'écrit : qui conduit bien sûr à . L'injectivité est donc établie.
- Montrons que l'application de
dans
définie par
n'est pas injective.
Prenons et . On vérifie les relations : et .
Le nombre a deux antécédents. L'application n'est pas injective. - Montrons que l'application de
dans
, définie par
n'est pas injective.
Prenons et . On vérifie les relations : et = -1).
Le nombre a deux antécédents. L'application n'est pas injective.
- Injectivité de \(g \circ f\)
- Injectivité de \(f \circ g\)
- Injectivité de \(g \circ f \circ h\)
Surjection
On dit qu'une application ou une fonction de dans est surjective ou une surjection de dans , si tout élément de admet au moins un antécédent dans , ce qui s'écrit avec des quantificateurs :
- Dans la pratique, on peut, pour un
quelconque dans
,
résoudre dans
l'équation (d'inconnue
) :
.
Si, pour tout dans , elle admet au moins une solution dans , alors est une surjection de sur . - Les ensembles et étant finis, n'est pas surjective si est strictement inférieur à .
- Une application
devient surjective si on limite l'ensemble d'arrivée à
.
Exemple : ( ). Comme l'équation n'a de solutions que pour tout positif, est une surjection de sur
La surjectivité dépend essentiellement de l'ensemble d'arrivée.
Soit quelconque dans , l'équation , avec est équivalente à , puis, si est différent de 2, à .
Tout différent de 2 a donc un antécédent et est une surjection de sur
- Surjectivité de \(g o f\)
- Surjectivité de \(f o g\)
- Surjectivité de \(g o f o h\)
Bijection
- Soient
et
deux ensembles.
On dit que est une application (ou une fonction) bijective ou une bijection de dans , si tout élément de admet exactement un antécédent dans , ce qui s'écrit avec des quantificateurs : - De cette définition, il découle que est bijective si et seulement si elle est injective et surjective.
- Si et sont deux ensembles finis tels que , ne peut pas être bijective.
- Si la bijection est donnée par un tableau, ce tableau possède autant de lignes que de colonnes et on n'observe qu'une seule étoile sur chaque ligne et sur chaque colonne. (Voir ici)
- Si la bijection est donnée par un diagramme sagittal, de chaque élément de l'ensemble de départ part une flèche et une seule, et chaque élément de l'ensemble d’arrivée est atteint par une flèche et une seule. (Voir ici)
- Pour une application donnée par une formule, pour un
quelconque dans
on peut résoudre dans
l'équation (d'inconnue
)
.
Si, pour tout dans , cette équation admet exactement une solution dans , alors est une bijection de dans
- Un exemple concret : L'application qui à une quantité d'essence achetée associe le prix payé est une bijection.
- La fonction de
dans
, définie par
n'est, on l'a vu, ni injective, ni surjective. En prenant sa restriction à
,
elle devient une application injective de
dans
qui n'est pas surjective.
Comme l'équation
admet dans
une unique solution (
), quel que soit y dans
, elle devient bijective
en tant qu'application de
dans
.
[De la même façon on aurait prouvé que c'est une application bijective de dans ]. - Soit un point d'un plan ; la symétrie centrale de centre est une bijection de dans . Le point a pour antécédent , et tout point de a pour antécédent le point de , unique symétrique de par rapport à .
- Considérons l'application de (ensemble des polynômes de degré inférieur ou égal à 2) dans (vecteurs de l'espace), qui à tout polynôme associe le vecteur de coordonnées . C'est ici un théorème, l'unicité de l'écriture d'un polynôme, qui fournit le caractère bijectif de cette application.
Elle est définie sur , à valeurs dans et un coup d’œil rapide sur une calculatrice graphique fournit une idée du résultat et de bons éléments de réponse !
Soit un réel quelconque strictement positif. Cherchons des solutions à l'équation . On obtient : . La fraction doit être positive ce qui conduit à imposer . Si l'on suppose cette double inégalité vérifiée, l'équation admet alors deux solutions .
Si l'on restreint l'ensemble de départ à (ou !), cette équation n'a plus qu'une seule solution, et ceci quel que soit dans l'intervalle
Conclusion : l'application est une bijection de (ou !) dans .
On demande à un groupe de personnes de laisser leur téléphone dans une boite à l'entrée d'une salle.
On note
l'ensemble des personnes,
l'ensemble des téléphones.
On s'intéresse au processus
qui met en relation une personne de
à son ou ses téléphones dans
.
Que faut-il supposer sur
et
pour que
soit une fonction ? une application ? une injection ? une surjection? une bijection?
- est une fonction à condition qu'aucune personne n'ait plus d'un téléphone...
- est une application si tout le monde a un téléphone.
- est une injection si aucun téléphone n'est partagé entre deux personnes...
- est une surjection, sauf si la veille quelqu'un, n'appartenant pas à ce groupe, a oublié son téléphone dans la boite...
- est une bijection si la boîte est vide au départ et si chacun a exactement un téléphone personnel.
- Reconnaissance d'applications 1
- Reconnaissance d'applications 2
- Tracé graphique d'applications
- Relations entre les notions d'injectivité, surjectivité et les cardinaux
- Relations, applications, injectivité, surjectivité et bijectivité
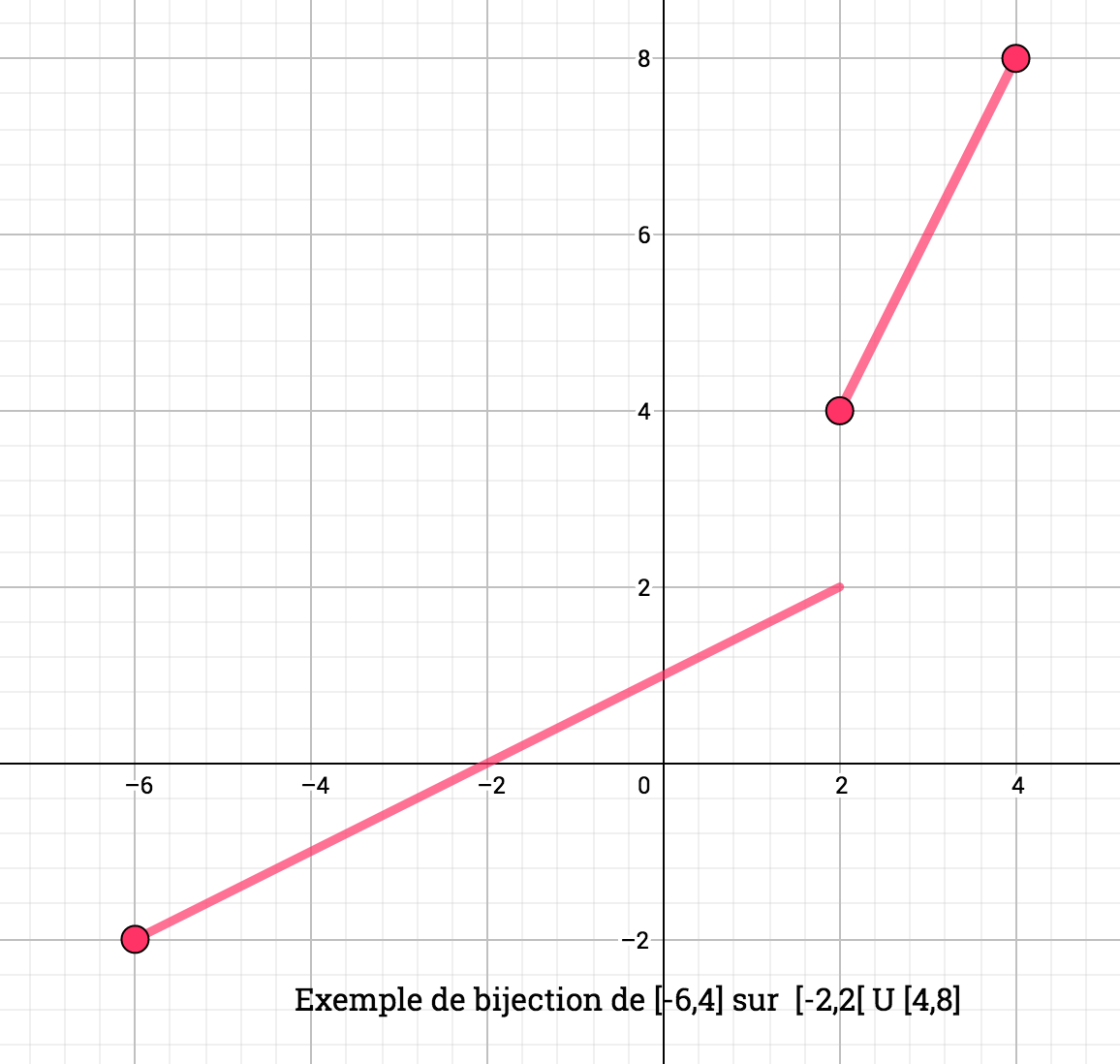
Exemples graphiques de bijection
Exemple de représentation graphique d'une bijection d'un ensemble vers un ensemble , donnée sous forme d'un diagramme sagittal.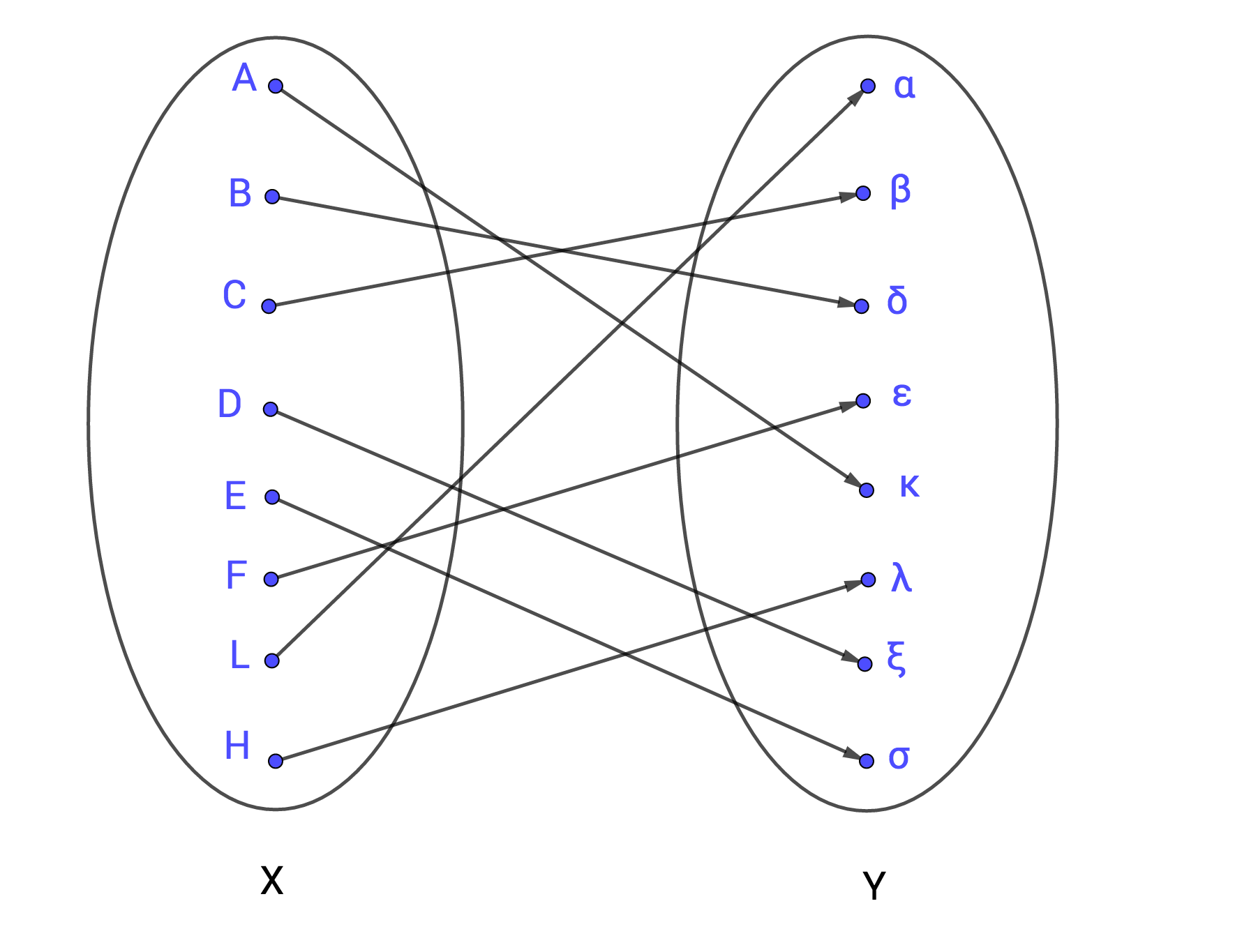
Théorèmes sur la bijection
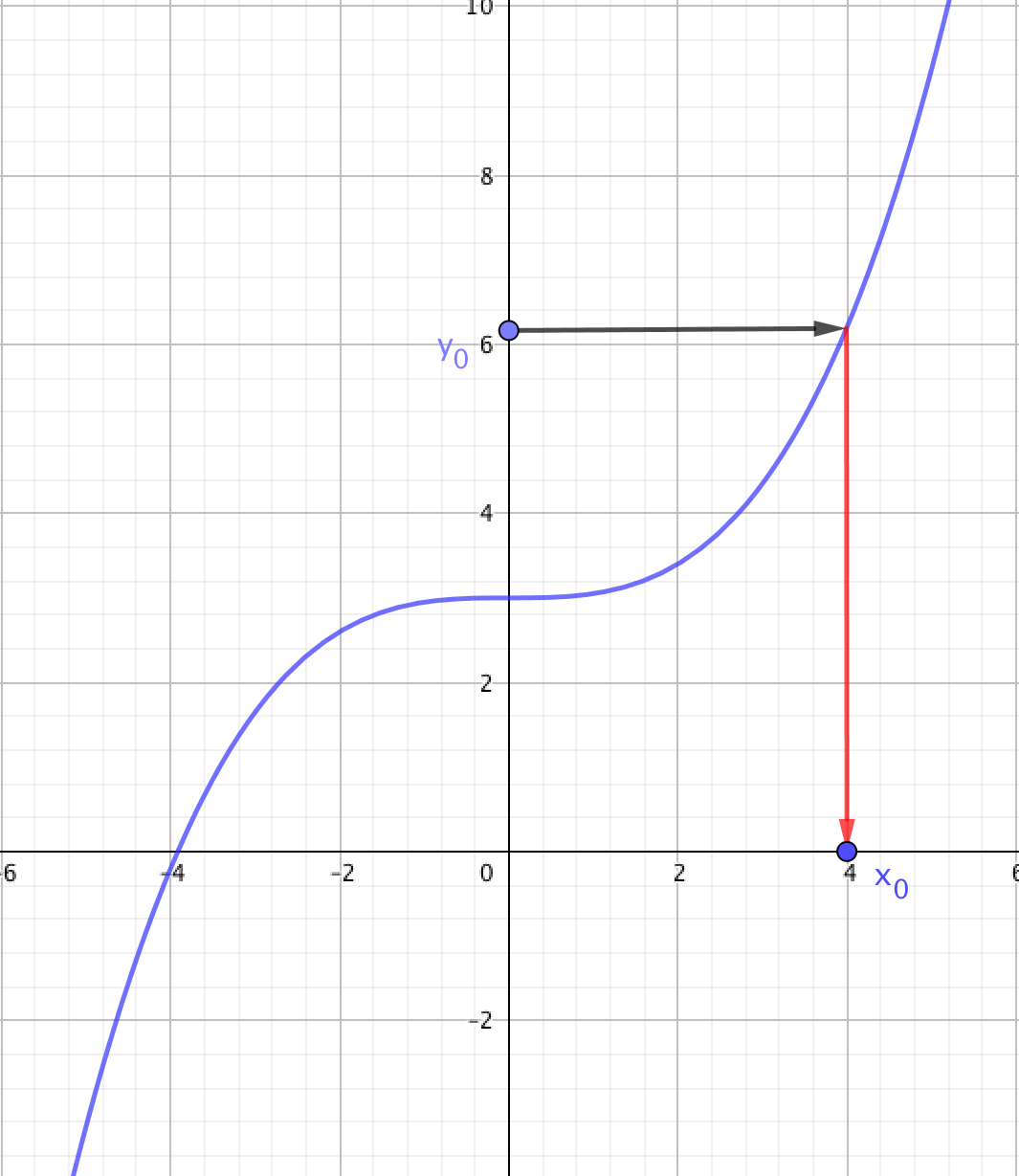
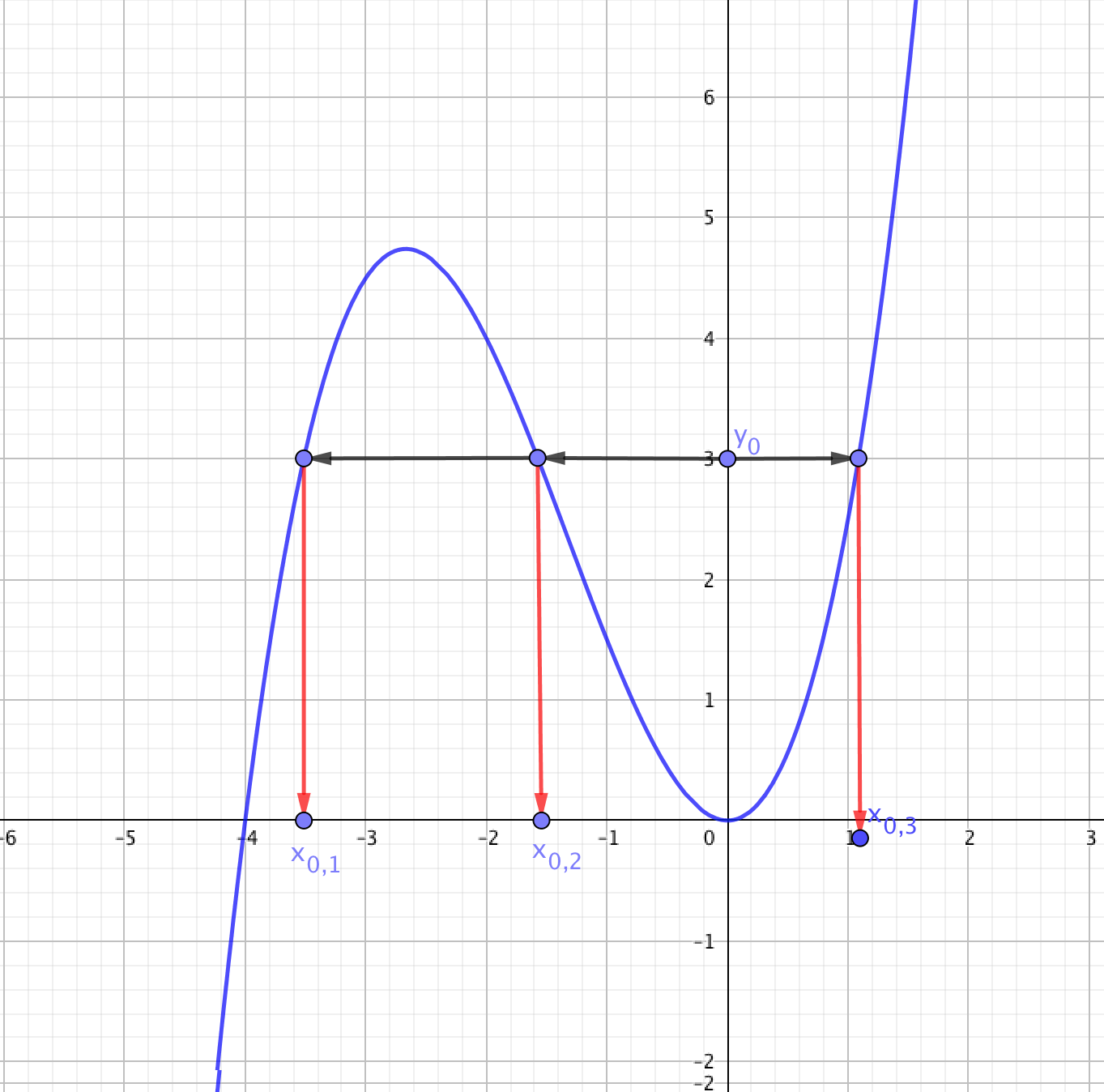
Si est une application strictement monotone sur un intervalle de , alors est une bijection de sur .
En d'autres termes, pour tout de , l'équation admet une unique solution dans .
Graphiquement, cela se visualise bien. Si la fonction n'est pas monotone, un réel de peut avoir plusieurs antécédents et la fonction n'est pas bijective, comme le montre le troisième dessin.
Cas particulier des fonctions dérivables.
Soit une application dérivable sur un intervalle de . Si, pour tout dans , la dérivée est, soit toujours strictement positive, soit toujours strictement négative, alors c'est une bijection de sur .
Bijection, bijection réciproque
Soient et deux ensembles. Si est une application bijective de dans , alors elle admet une application réciproque de dans , notée , qui est également bijective. On a l'équivalence :
- L'application de dans est bijective et admet l'application de dans pour application réciproque.
- L'application de dans qui à associe est bijective et admet pour réciproque l'application de dans qui à associe .
- Dans un plan, la symétrie orthogonale par rapport à une droite est bijective et admet elle-même pour application réciproque : .
- Reprenons l'exemple 2 de cette
page
:
.
L’antécédent (unique) de tout réel différent de 2 est . L'application réciproque est donc l'application :
: , définie pour tout par : . Ou si l'on préfère : , la variable d'une fonction étant une lettre muette à laquelle toute autre est substituable.
Montrer que est une bijection de sur son image (que l'on déterminera), et trouver son application réciproque.
- est l'intervalle ouvert
- Chercher l'application réciproque
- Dans cet exercice , des questions sur une "fonction quadratique" (= fonction polynôme du second degré) sont posées : définition, injectivité, surjectivité. On peut s'aider d'un calculateur graphique.
- Calcul de valeurs pour \(f^{-1}\)
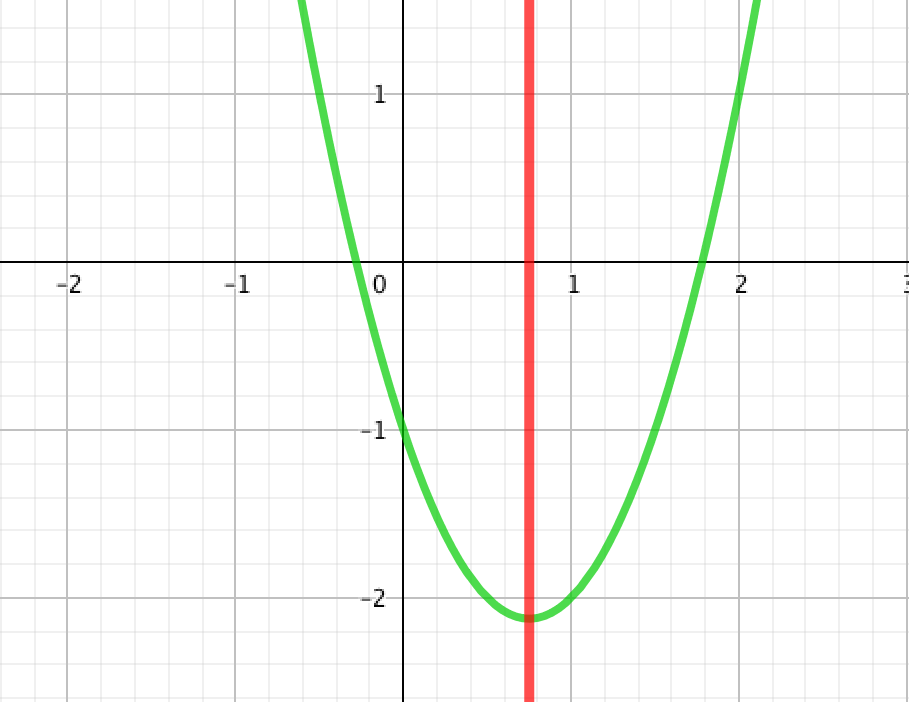
Fonctions paires
- On dit qu'une fonction
de
dans
est paire, si
- ,
- vérifie la propriété : , .
- On munit le plan d'un repère orthonormé . La courbe représentative d'une application de dans est symétrique par rapport à la droite d'équation , si vérifie :
, ou de façon équivalente
Dans un repère orthonormé, la représentation graphique d'une fonction paire est symétrique par rapport à l'axe des ordonnées (symétrie axiale).
Les fonctions suivantes de
dans
sont-elles paires ?
,
,
,
,
,
,
,
Fonctions impaires
- On dit qu'une fonction
de
dans
est impaire, si
- ,
- ,
- La courbe représentative d'une application de dans admet le point de coordonnées pour centre de symétrie, si vérifie :
, ou de façon équivalente
-
,
,
,
,
, , , - Montrer que la fonction de
dans
définie par
, définie pour
admet un centre de symétrie que l'on déterminera.
On écrit, pour la fonction donnée, l'égalité . On simplifie l'écriture jusqu'à arriver à un trinôme du second degré nul (dont les coefficients doivent donc être nuls, à cause de l'unicité de l'écriture d'un polynôme). Le résultat est le point .
Fonctions périodiques
- La fonction est périodique de période
- Les fonctions "créneau" que l'on trouve en physique, comme celle-ci, de période 1.
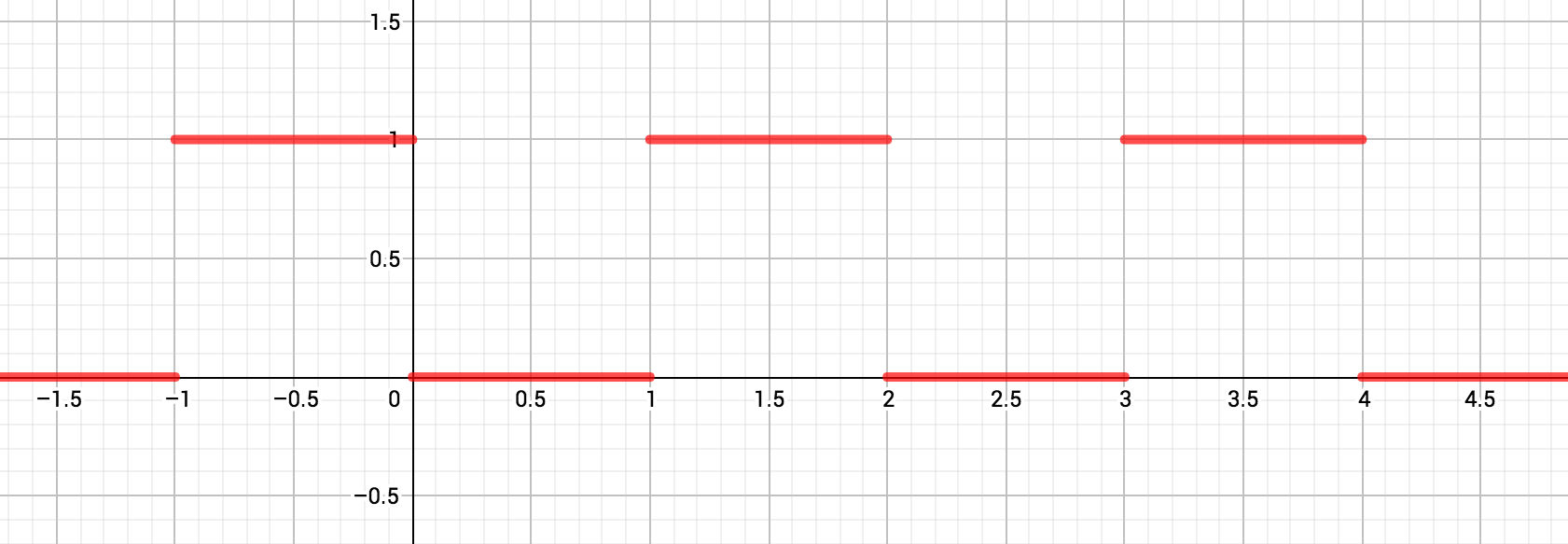
- La fonction définie par :
. Quelle semble en être la période ?
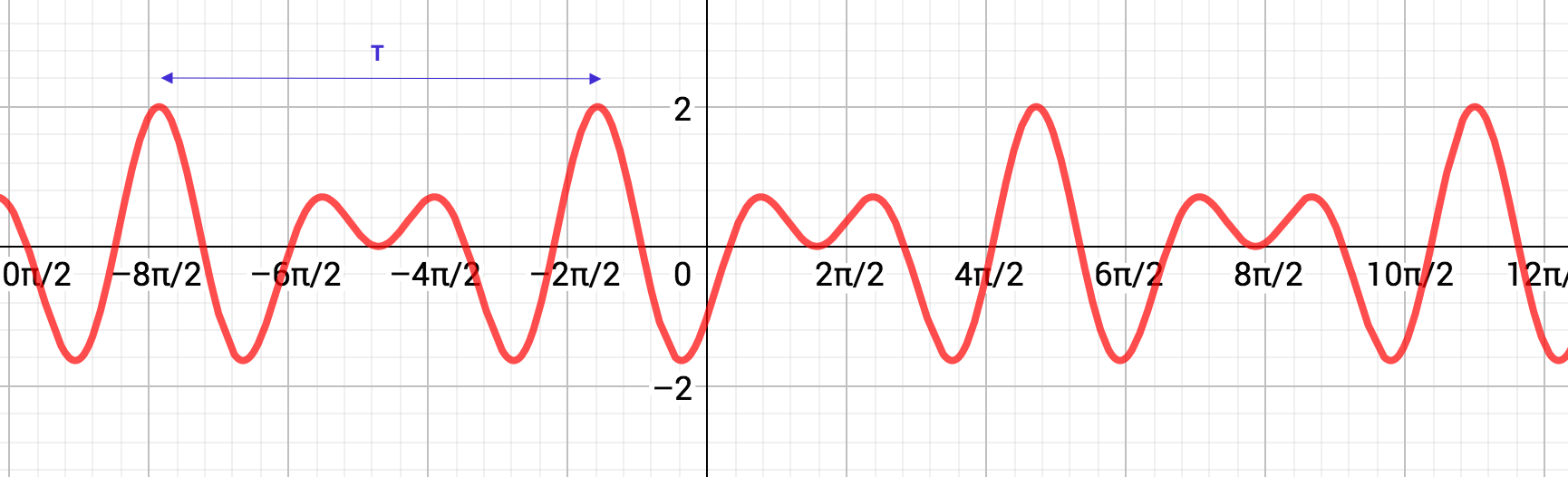
Quelle est la plus petite période des fonctions suivantes, définies de dans ?
, , .
Pour tout réel, il existe un entier tel que . Par définition, on pose .
La partie entière d'un réel est donc le plus grand entier inférieur ou égal à .
Translations
Rappel : Définition et propriétés d'une translation- Soit
un réel quelconque, dans un repère orthonormé
, l'image de la courbe
d'une fonction
par
une translation de vecteur
, est la courbe
de la fonction
définie par :
,
- Soit
un réel quelconque, l'image de la courbe
d'une fonction
par
une translation de vecteur
, est la courbe
de la fonction
, définie par :
,
Translation horizontale : Changement de en
Soit un réel, une fonction et la fonction définie par . Alors la courbe représentative de s'obtient à partir de celle de en lui faisant subir une translation de vecteur .
Translation verticale
Soit un réel, une fonction et la fonction définie par . Alors la courbe représentative de s'obtient à partir de celle de en lui faisant subir une translation de vecteur .
Transformations opérant sur une représentation graphique
On se place dans le plan rapporté à un repère orthonormé .
Changement de en
Le changement de en dans l'écriture d'une fonction symétrise la représentation graphique de la fonction par rapport à l'axe des ordonnées.
Changement de en puis en
On considère la fonction définie par . Elle est tracée en rouge. En bleu, on a tracé la courbe de la fonction avec . En orange, la courbe de , avec Ces transformations s'appellent des affinités. Elles correspondent à des "dilatations", à partir de la courbe de , verticalement pour et horizontalement pour .
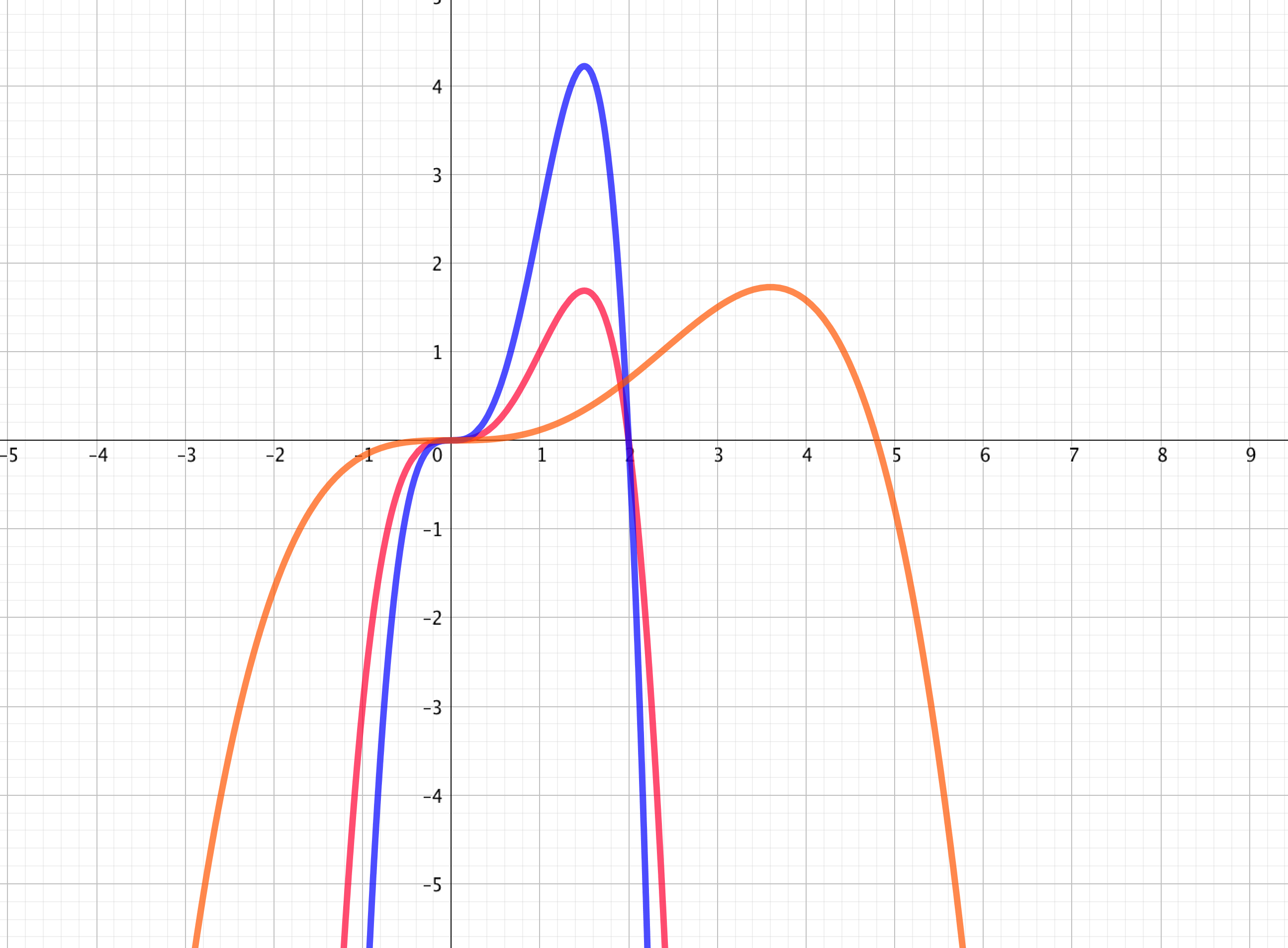
Dans cet exercice, il s'agit , à partir de la représentation graphique d'une fonction définie par , d'identifier les représentations graphiques des fonctions définies par :
Bibliographie
Livres
- F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 1
- Annick Auzimour et Frédérique Petit, Travaux dirigés d'algèbre (Vuibert).
- Anne Denmat et Francis Héaulme, Algèbre générale (Dunod).
Cours WIMS
- DOC Raisonnements
- Doc Ensembles
- Isométries du plan