Patrons d'un polyèdre convexe
Patrons d'un polyèdre convexe
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
On s'intéresse ici aux polyèdres convexes et à la manière de les construire à partir d'une feuille de papier, ce qu'on appelle un patron. Pour la définition d'un polyèdre convexe, voir le document Doc Polyèdres convexes semi-réguliers .
Nous parlerons donc des sommets, des arêtes et des faces du polyèdre. En particulier, chaque face est contenue dans un plan qui divise l'espace en deux régions et le polyèdre est convexe si, pour chacune de ses faces, il se trouve entièrement dans l'une des régions délimitée par le plan qui contient cette face.
Voir aussi l'outil de visualisation Polyèdres convexes montre des polyèdres convexes et leurs patrons.
Algorithme d'obtention de patrons
Graphe associé à un polyèdre
Patrons d'un polyèdre convexe
→ Graphe associé à un polyèdre
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
On associe à un polyèdre
un graphe
de la manière suivante.
Les sommets du graphe
sont les faces du polyèdre
et deux sommets du graphe
sont reliés si les deux faces correspondantes
de
ont une arête commune. Les arêtes de
correspondent aux arêtes
du graphe
. Le graphe
est connexe.
Si est la matrice d'adjacence de (une fois choisi un ordre dans la liste des faces de , ce que nous supposerons désormais), le nombre de 1 sur une ligne (et sur une colonne) est le nombre de côtés de la face correspondante.
Nous parlerons de polyèdre combinatoire quand seules sont connues ou utilisées les données du graphe et pas les coordonnées dans : plus précisément, c'est un graphe augmenté de la donnée de cycles qu'on appelle faces, chaque arête apparaissant dans exactement deux cycles, une fois dans chaque sens.
Exemple [ Tétraèdre ]
Exemple [ Cube ]
Voici un cube
La matrice d'adjacence du graphe associé au cube est
Le graphe a 6 sommets et les 6 faces du cube sont des carrés.
On peut représenter son graphe de la manière suivante:
![]()
Exemple [ Dodécaèdre régulier ]
Exemple [ Cuboctaèdre ]
Si est la matrice d'adjacence de (une fois choisi un ordre dans la liste des faces de , ce que nous supposerons désormais), le nombre de 1 sur une ligne (et sur une colonne) est le nombre de côtés de la face correspondante.
Nous parlerons de polyèdre combinatoire quand seules sont connues ou utilisées les données du graphe et pas les coordonnées dans : plus précisément, c'est un graphe augmenté de la donnée de cycles qu'on appelle faces, chaque arête apparaissant dans exactement deux cycles, une fois dans chaque sens.
Exemple [ Tétraèdre ]
Voici un tétraèdre
La matrice d'adjacence du graphe associé au tétraèdre est
Ce graphe a 4 sommets et les 4 faces du tétraèdre sont des triangles.
On peut représenter son graphe de la manière suivante:
![]()
La matrice d'adjacence du graphe associé au tétraèdre est
Exemple [ Cube ]
Voici un cube
La matrice d'adjacence du graphe associé au cube est
On peut représenter son graphe de la manière suivante:
Exemple [ Dodécaèdre régulier ]
Voici un dodécaèdre:
La matrice d'adjacence du graphe associé au dodécaèdre régulier est
Le graphe a 12 sommets et les 12 faces du dodécaèdre régulier sont des pentagones.
On peut représenter son graphe de la manière suivante:
![]()
La matrice d'adjacence du graphe associé au dodécaèdre régulier est
On peut représenter son graphe de la manière suivante:
Exemple [ Cuboctaèdre ]
Voici un cuboctaèdre ou cube tronqué:
La matrice d'adjacence du graphe associé au cuboctaèdre est
Le graphe du cuboctaèdre a 14 sommets, 6 des faces du cuboctaèdre sont des carrés et 8 d'entre elles
sont des triangles.
Le graphe associé peut être représenté de la manière suivante:
![]()
La matrice d'adjacence du graphe associé au cuboctaèdre est
Le graphe associé peut être représenté de la manière suivante:
Patrons d'un polyèdre convexe
→ Graphe associé à un polyèdre
Patron
Patrons d'un polyèdre convexe
→ Patron
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Patrons d'un polyèdre convexe
→ Patron
Technique de confection d'un patron
Patrons d'un polyèdre convexe
→
Patron
→ Technique de confection d'un patron
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Commençons par une description concrète (nous ne formaliserons pas
la définition, rappelons la définition du dictionnaire encyclopédique
Quillet:
patron: Modèle sur lequel ou d'après lequel on travaille.
Morceau de papier que les tailleurs, les couturières, les brodeuses,
etc découpent de manière à figurer les
différentes parties de leur ouvrage et d'après lequel ils taillent
l'étoffe dont ces ouvrages doivent être faits;
nous rajouterons ici que l'on désire ensuite faire le moins de coutures possibles).
On désire construire un polyèdre convexe à l'aide d'une feuille de papier. Pour cela, on doit aplatir le polyèdre en découpant certaines arêtes. Il faut découper suffisamment d'arêtes pour pouvoir l'étaler sur une feuille de papier et pas trop pour qu'il n'y ait qu'un seul morceau. Il faut aussi que les différents polygones obtenus à partir des faces du polyèdre ne se chevauchent pas. On appelle le résultat un patron du polyèdre. C'est donc une réunion de polygones dans le plan tels que l'intersection de deux de ces polygones est soit vide, soit un sommet commun, soit une arête commune. On désigne encore ces polygones par le nom de faces du patron. Les arêtes du polyèdre qui ne sont pas découpées deviennent des côtés communs à deux des faces (arêtes de pliage du patron). Les arêtes qui sont découpées deviennent deux côtés du bord du patron. Lorsque la condition de non-chevauchement n'est pas vérifiée, nous parlerons de pseudo-patron.
On conjecture que tout polyèdre convexe a au moins un patron (Albrecht Dürer (1525), énoncé comme une conjecture en 1975 par G. Shephard Shephard ).
On associe à un patron (ou à un pseudo-patron) un graphe : ses sommets sont les faces du patron et deux sommets sont reliés dans le graphe si les faces ont un côté commun dans le patron. Les faces du polyèdre correspondent aux faces du patron, l'ensemble des arêtes du graphe du patron (arêtes de pliages du patron) est un sous-ensemble des arêtes du graphe associé du polyèdre. Donc, est un sous-graphe du graphe du polyèdre .
Quand on a bien découpé le polyèdre, on peut aller d'un sommet à un autre (connexité), d'une seule manière (acyclicité): le graphe associé est ce qu'on appelle un arbre couvrant de .
On désire construire un polyèdre convexe à l'aide d'une feuille de papier. Pour cela, on doit aplatir le polyèdre en découpant certaines arêtes. Il faut découper suffisamment d'arêtes pour pouvoir l'étaler sur une feuille de papier et pas trop pour qu'il n'y ait qu'un seul morceau. Il faut aussi que les différents polygones obtenus à partir des faces du polyèdre ne se chevauchent pas. On appelle le résultat un patron du polyèdre. C'est donc une réunion de polygones dans le plan tels que l'intersection de deux de ces polygones est soit vide, soit un sommet commun, soit une arête commune. On désigne encore ces polygones par le nom de faces du patron. Les arêtes du polyèdre qui ne sont pas découpées deviennent des côtés communs à deux des faces (arêtes de pliage du patron). Les arêtes qui sont découpées deviennent deux côtés du bord du patron. Lorsque la condition de non-chevauchement n'est pas vérifiée, nous parlerons de pseudo-patron.
On conjecture que tout polyèdre convexe a au moins un patron (Albrecht Dürer (1525), énoncé comme une conjecture en 1975 par G. Shephard Shephard ).
On associe à un patron (ou à un pseudo-patron) un graphe : ses sommets sont les faces du patron et deux sommets sont reliés dans le graphe si les faces ont un côté commun dans le patron. Les faces du polyèdre correspondent aux faces du patron, l'ensemble des arêtes du graphe du patron (arêtes de pliages du patron) est un sous-ensemble des arêtes du graphe associé du polyèdre. Donc, est un sous-graphe du graphe du polyèdre .
Quand on a bien découpé le polyèdre, on peut aller d'un sommet à un autre (connexité), d'une seule manière (acyclicité): le graphe associé est ce qu'on appelle un arbre couvrant de .
Patrons d'un polyèdre convexe
→
Patron
→ Technique de confection d'un patron
Patron et arbre couvrant
Patrons d'un polyèdre convexe
→
Patron
→ Patron et arbre couvrant
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Rappelons quelques définitions (voir le document
Graphes
pour des explications
plus complètes).
Si
est un graphe connexe, un graphe couvrant de
est un graphe dont les sommets sont exactement les sommets
de
et dont les arêtes forment un sous-ensemble de celles de
.
Un arbre couvrant d'un graphe connexe est un graphe couvrant qui
est un arbre, c'est-à-dire qu'il est connexe et acyclique.
Soit un patron de d'arbre couvrant . Soient , et le nombre de sommets, de faces et d'arêtes du polyèdre et soient , ..., les nombres de sommets des faces du polyèdre.
Exemple
Exemple
Exemple
Soit un patron de d'arbre couvrant . Soient , et le nombre de sommets, de faces et d'arêtes du polyèdre et soient , ..., les nombres de sommets des faces du polyèdre.
- Le graphe de a sommets et arêtes.
- L'arbre a sommets et arêtes (comme tout arbre).
- Le patron a faces (correspondant aux sommets de et aux faces de ) et arêtes (arêtes de pliage).
- On obtient un patron en partant d'une face à
sommets et en recollant une à une
les autres faces. Cette opération ajoute
nouveaux sommets.
Le nombre de sommets de
est donc
- Le nombre d'arêtes de est égal à .
- Le nombre de sommets de est égal à .
Exemple
Rappelons que la matrice du graphe du tétraèdre est
Il a
arêtes.
Cherchons des matrices correspondant à un arbre couvrant du tétraèdre.
Comme un arbre est connexe et sans cycle,
on doit couper au moins
arêtes pour qu'il n'y ait plus de cycles
et au plus
pour qu'il reste connexe.
Le graphe des matrices suivantes a
arêtes et correspond à des arbres
couvrants du graphe du tétraèdre. Voici deux exemples.




Exemple
Exemple
Patrons d'un polyèdre convexe
→
Patron
→ Patron et arbre couvrant
Fonction associée à un arbre couvrant (ou à un patron)
Patrons d'un polyèdre convexe
→
Patron
→ Fonction associée à un arbre couvrant (ou à un patron)
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Numérotons de 1 à
les faces du polyèdre.
Choisissons une face
du polyèdre.
Nous allons associer à un patron
une fonction de
dans lui-même de la manière suivante.
Soit
une face. Il existe un seul chemin simple allant
de
à
. On définit
comme la première étape sur ce chemin.
Par convention,
.
On obtient ainsi une fonction de dans lui-même telle que et que pour tout , il existe tel que .
Toute fonction de ce type donne un graphe dont la matrice d'adjacence vérifie que si et seulement si ( ou ) et . Ce graphe est un arbre couvrant car il est clairement connexe et a arêtes (cf. Graphes ).
On coupe les arêtes du polyèdre séparant deux faces et si et seulement si et . Cela permet d'étaler le polyèdre sur un plan. Si les morceaux de papier obtenus ne se chevauchent pas, on a obtenu un patron. Sinon, c'est juste un pseudo-patron. Par exemple, la matrice associée à l'arbre couvrant tel que , , , est
On note une telle fonction
par
.
Exemple
Exemple
Exemple
On obtient ainsi une fonction de dans lui-même telle que et que pour tout , il existe tel que .
Toute fonction de ce type donne un graphe dont la matrice d'adjacence vérifie que si et seulement si ( ou ) et . Ce graphe est un arbre couvrant car il est clairement connexe et a arêtes (cf. Graphes ).
On coupe les arêtes du polyèdre séparant deux faces et si et seulement si et . Cela permet d'étaler le polyèdre sur un plan. Si les morceaux de papier obtenus ne se chevauchent pas, on a obtenu un patron. Sinon, c'est juste un pseudo-patron. Par exemple, la matrice associée à l'arbre couvrant tel que , , , est
Exemple
[
]
Exemple
[
]
Exemple
[
]
Patrons d'un polyèdre convexe
→
Patron
→ Fonction associée à un arbre couvrant (ou à un patron)
Algorithme d'obtention de patrons
Patrons d'un polyèdre convexe
→ Algorithme d'obtention de patrons
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Patrons d'un polyèdre convexe
→ Algorithme d'obtention de patrons
Calcul d'un arbre couvrant
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Calcul d'un arbre couvrant
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
On peut facilement énumérer toutes les fonctions
de
dans lui même,
et tester pour chacune si elle vérifie la condition
que
et que pour tout
, il existe
tel que
.
Mais leur nombre pouvant être énorme,
il est utile de pouvoir en choisir une au hasard.
L'algorithme suivant de A. Broder Generating random spanning trees A. Broder 30th Annual Symposium on Foundations of Computer Science Year: 1989 | Conference Paper | Publisher: IEEE permet de trouver un arbre couvrant aléatoire de manière uniformément distribuée.
On simule une marche aléatoire simple sur le graphe en partant du sommet
(racine)
jusqu'à ce que tout sommet soit visité. Autrement dit:
On obtient un arbre couvrant car
est connexe avec
sommets
et
arêtes (une pour chaque arête différente de
).
On montre qu'il est uniformément distribué.
Exemple
L'algorithme suivant de A. Broder Generating random spanning trees A. Broder 30th Annual Symposium on Foundations of Computer Science Year: 1989 | Conference Paper | Publisher: IEEE permet de trouver un arbre couvrant aléatoire de manière uniformément distribuée.
On simule une marche aléatoire simple sur le graphe en partant du sommet
(racine)
jusqu'à ce que tout sommet soit visité. Autrement dit:
- On part du sommet
.
- À chaque étape, on choisit un voisin aléatoirement et de manière uniforme.
- À chaque fois qu'on visite un nouveau sommet
, on rajoute dans
le sommet
et l'arête où est le sommet d'où l'on vient.
Exemple
Prenons le graphe du cube (voir exemple
cube
)
et la marche aléatoire suivante
.
Les nouveaux sommets apparaissent dans l'ordre
,
,
,
,
,
. La racine est 1.
Les arêtes de l'arbre couvrant sont celles de leur première apparition,
c'est-à-dire
,
,
,
,
.
La fonction associée est donnée par
.
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Calcul d'un arbre couvrant
Préliminaires géométriques
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Préliminaires géométriques
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
On travaille dans l'espace euclidien
de base canonique
ou dans le plan euclidien
vu comme le plan d'équation
orthogonal à
.
et on a
On veut donc envoyer (
,
,
)
sur (
,
,
).
La matrice de (
,
,
)
dans la base
est
avec
.
En posant
et
,
la matrice de (
,
,
)
dans la base
est
La matrice de la transformation dans la base canonique
est donc
.
La troisième colonne de
est la troisième colonne de
(autrement dit
) puisqu'on envoie
sur
.
Lemme
Soient
et
deux vecteurs de
de même norme.
Il existe une unique
rotation qui envoie
sur
. Elle est donnée par
avec
et
.
Lemme
Soient
et
deux vecteurs non colinéaires de
. La base
donnée par
,
,
est une base orthonormée directe. Les plans
et
sont égaux
avec même orientation.
Lemme
Soient
et
deux vecteurs unitaires de
et
(resp.
) un vecteur unitaire orthogonal à
(resp.
).
Il existe une unique
rotation qui envoie
sur
et
sur
.
Soit
(resp.
) tel que
(resp.
) soit une base orthonormée directe.
Il existe une unique rotation envoyant une base orthonomormée directe sur une autre.
Explicitement, si
(resp.
) est la matrice de
(resp. de
)
dans la base
canonique, la matrice de la rotation
est donnée par
.
Lemme
Soient deux points distincts
et
dans
et
un vecteur unitaire orthogonal à
. Soient deux points
et
du plan d'équation
tels que
et
soient de même longueur. Soit
.
Soit
le vecteur unitaire du plan orthogonal à
,
faisant un angle
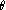 avec
et tel que
soit direct (
).
Il existe un unique déplacement qui envoie
sur
et le vecteur
sur
.
avec
et tel que
soit direct (
).
Il existe un unique déplacement qui envoie
sur
et le vecteur
sur
.
Nous allons le calculer explicitement.
Pour simplifier les formules, supposons que
et
sont unitaires.
Le vecteur
est donné par
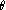 avec
et tel que
soit direct (
).
Il existe un unique déplacement qui envoie
sur
et le vecteur
sur
.
avec
et tel que
soit direct (
).
Il existe un unique déplacement qui envoie
sur
et le vecteur
sur
.
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Préliminaires géométriques
Calcul des coordonnées des sommets du patron
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Calcul des coordonnées des sommets du patron
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Supposons le polyèdre
donné par les coordonnées de ses sommets
et par la liste de ses faces: chaque face est donnée par la liste
de ses sommets consécutifs orientée par une normale extérieure au polyèdre,
c'est-à-dire que si les sommets sont
,
pour
et
sont des normales extérieures à la face.
Fixons une face, par exemple la dernière dans la liste des faces, nommée . Soit un arbre couvrant du graphe des faces donné par la fonction en direction de : si est une face, est la face suivant si l'on désire aller de la face à la face . Le but est donc d'avoir la liste des coordonnées des sommets du patron et la liste des faces.
On commence par la face que l'on déplace dans le plan d'équation . On va ensuite rajouter les faces une à une. Expliquons comment on ajoute à une face déjà calculée une face non encore calculée telle que .
Fixons une face, par exemple la dernière dans la liste des faces, nommée . Soit un arbre couvrant du graphe des faces donné par la fonction en direction de : si est une face, est la face suivant si l'on désire aller de la face à la face . Le but est donc d'avoir la liste des coordonnées des sommets du patron et la liste des faces.
On commence par la face que l'on déplace dans le plan d'équation . On va ensuite rajouter les faces une à une. Expliquons comment on ajoute à une face déjà calculée une face non encore calculée telle que .
- On calcule l'arête du polyèdre de la face telle que est une arête de la face . On connait les sommets et correspondants sur le patron.
- On calcule alors le déplacement qui envoie les sommets et du polyèdre sur les sommets et du patron et la normale extérieure unitaire à la face sur le vecteur unitaire (lemme deptheta avec ).
- On l'applique à tous les sommets de la face . Cela permet donc de tracer l'image de la face dans le patron dans le plan d'équation .
- S'il y a un chevauchement de cette face avec les autres faces déjà calculées, on rejette l'arbre couvrant en question car il correspond à un pseudo-patron et non à un patron. Sinon, on continue à ajouter les nouvelles faces jusqu'à épuisement des faces du polyèdre.
Patrons d'un polyèdre convexe
→
Algorithme d'obtention de patrons
→ Calcul des coordonnées des sommets du patron
Retrouver le polyèdre à partir du patron
Patrons d'un polyèdre convexe
→ Retrouver le polyèdre à partir du patron
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
On a maintenant un arbre couvrant et le patron associé.
On cherche à replier le patron pour obtenir le polyèdre.
Les données sont donc maintenant
Supposons qu'une face numéro de soit déjà calculée ainsi qu'une normale unitaire et que la face numéro de où n'ait pas été encore calculée. On calcule l'arête du polyèdre de la face telle que est une arête de la face . On connait l'arête (resp. ) correspondante sur (resp. ). Le lemme deptheta avec
- les coordonnées des sommets et les faces du polyèdre;
- les coordonnées des sommets et les faces du patron, celles-ci étant dans le même ordre que les faces du polyèdre;
- la correspondance entre les sommets du patron et les sommets du polyèdre;
- pour chaque face du polyèdre, sa normale unitaire extérieure .
Supposons qu'une face numéro de soit déjà calculée ainsi qu'une normale unitaire et que la face numéro de où n'ait pas été encore calculée. On calcule l'arête du polyèdre de la face telle que est une arête de la face . On connait l'arête (resp. ) correspondante sur (resp. ). Le lemme deptheta avec
- , ,
- la normale extérieure de la face numéro de ,
-
avec
 l'angle entre les faces numéro
et
du polyèdre
l'angle entre les faces numéro
et
du polyèdre
Patrons d'un polyèdre convexe
→ Retrouver le polyèdre à partir du patron
Exemples
Patrons d'un polyèdre convexe
→ Exemples
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Patron associé à l'arbre couvrant représenté par []
Patrons d'un polyèdre convexe
→ Exemples
Dualité
Patrons d'un polyèdre convexe
→ Dualité
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
Soit
un polyèdre combinatoire.
Le polyèdre combinatoire dual
de
est obtenu de la manière suivante.
On associe à chaque face
de
un sommet
de
.
Soit
un sommet de
. Soit
l'ensemble des faces auquel
appartient, ordonné de manière à ce que
On associe au sommet la face de et on associe à une arête de entre les faces et l'arête de qui relie les sommets et .
Les sommets du graphe associé à (qui sont les faces de ) sont donc en bijection naturelle avec les sommets de .
Une construction géométrique du polyèdre dual d'un polyèdre convexe est la suivante. On part du centre du polyèdre (convexe), c'est-à-dire l'isobarycentre des sommets. On considère une sphère de centre et de rayon , par exemple 1. On définit géométriquement le polyèdre dual par polarité par rapport à cette sphère: à chaque sommet , on associe le plan perpendiculaire au segment et tel que le produit des distances algébriques de à et à est égale à . Le polyèdre dual est le polyèdre convexe dont les faces sont contenues dans les plans . La face du polyèdre dual associée à est la face contenue dans le plan .
À un arbre couvrant du graphe associé à , on associe un arbre couvrant du graphe associé à de la manière suivante. Si l'arbre de est obtenu en supprimant le sous-ensemble d'arêtes de , l'arbre couvrant associé est obtenu en supprimant le complémentaire de l'image de dans l'ensemble des arêtes de . Ainsi, à tout pseudo-patron de obtenu en découpant les arêtes appartenant à , on fait correspondre le pseudo-patron de obtenu en découpant les arêtes de "croisant" (par projection sur la sphère) celles de qui ne sont pas dans .
Exemples
- et ont une arête commune
- si , le successeur de dans la face est (cela restera alors vrai pour ).
On associe au sommet la face de et on associe à une arête de entre les faces et l'arête de qui relie les sommets et .
Les sommets du graphe associé à (qui sont les faces de ) sont donc en bijection naturelle avec les sommets de .
Une construction géométrique du polyèdre dual d'un polyèdre convexe est la suivante. On part du centre du polyèdre (convexe), c'est-à-dire l'isobarycentre des sommets. On considère une sphère de centre et de rayon , par exemple 1. On définit géométriquement le polyèdre dual par polarité par rapport à cette sphère: à chaque sommet , on associe le plan perpendiculaire au segment et tel que le produit des distances algébriques de à et à est égale à . Le polyèdre dual est le polyèdre convexe dont les faces sont contenues dans les plans . La face du polyèdre dual associée à est la face contenue dans le plan .
À un arbre couvrant du graphe associé à , on associe un arbre couvrant du graphe associé à de la manière suivante. Si l'arbre de est obtenu en supprimant le sous-ensemble d'arêtes de , l'arbre couvrant associé est obtenu en supprimant le complémentaire de l'image de dans l'ensemble des arêtes de . Ainsi, à tout pseudo-patron de obtenu en découpant les arêtes appartenant à , on fait correspondre le pseudo-patron de obtenu en découpant les arêtes de "croisant" (par projection sur la sphère) celles de qui ne sont pas dans .
Exemples
Patrons d'un polyèdre convexe
→ Dualité
Bibliographie
Patrons d'un polyèdre convexe
→ Bibliographie
- Graphe associé à un polyèdre
- Patron
- Algorithme d'obtention de patrons
- Retrouver le polyèdre à partir du patron
- Exemples
- Dualité
- Bibliographie
La bibliographie est très partielle. Beaucoup de sites internet parlent de ce sujet.
Le but de ce document est simplement de présenter les algorithmes que nous
avons utilisés pour permettre d'obtenir des patrons à découper
(par exemple en tikz dans
Polyèdres convexes
).
- [Broder] Broder, A., Generating random spanning trees, 30th Annual Symposium on Foundations of Computer Science Year: 1989 | Conference Paper | Publisher: IEEE
- [Dürer] Dürer, A., Unterweisung der Messung mit dem Zirkel und Richtscheit, 1525. English translation and commentary, W. Strauss, The Painter's Manual, Abaris, New York, 1977.
- [Shephard] Shephard, G., Convex polytopes with convex nets, Math. Proc. Camb. Phil. Soc. 78 (1975) 389-403.
Patrons d'un polyèdre convexe
→ Bibliographie