OEF 多项式
--- 介绍 ---
本模块目前包含 32 个关于实或复系数单变量多项式的练习:
根, 次数, 复合, 带余除法, ...
与导数的最大公因式次数
设 P(x) 是一个 次系数多项式, 它有 个不同的实根和 个不同的复根 (不计重数). 设 P'(x) 是 P(x) 的导数. 问 gcd(P(x),P'(x)) 的次数是多少?
有重根的最小次数
满足以下条件的系数多项式 P(x) 的最小次数是多少? 如果你认为这样的多项式不存在. 则回答 -1.
和的次数
设 () 和 () 是两个多项式. 问: 若 deg()= 及 deg()=, 则 是一个多项式, 它的次数为
差分方程
求多项式 () 使得 ()-() = 2 且 ()=.
我们用 x^3 代表 3, 如此类推.
3 次多项式的重根
以下多项式有一个重根. 试求出这个根.
4 次多项式的重根
以下多项式有一个重根. 试求出这个根.
5 次多项式的重根
以下多项式有一个重根. 试求出这个根.
6 次多项式的重根
以下多项式有一个重根. 试求出这个根.
已知与导数的最大公因式
求出多项式 () 使得: - gcd((),()) = ()() , 这里 () 是 () 的导数;
- ()= ;
- 的次数尽可能小.
你输入的多项式写成因式乘积或展开的形式均可接受. 我们用 x^3 代表 3, 如此类推.
已知3次多项式的根
求多项式 P() = 32 , 已知 和 是实数, 是一个根.
与2阶导数的最大公因式的最小次数
设 P(x) 是一个 次系数多项式, 它有 个不同实根与 个不同复根 (不计重数). 设 P''(x) 是 P(x) 的 2 阶导数. 问最大公因式 gcd(P(x),P''(x)) 次数的最小值是多少?
与高阶导数的最大公因式的最小次数
设 P(x) 是一个 次系数多项式, 它有 个不同实根与 个不同复根 (不计重数). 设 P()(x) 是 P(x) 的 阶导数. 问最大公因式 gcd(P(x),P()(x)) 次数的最小值是多少?
3 次多项式根的重数
是以下多项式的一个根. 求它的重数.
4 次多项式根的重数
是以下多项式的一个根. 求它的重数.
5 次多项式根的重数
是以下多项式的一个根. 求它的重数.
6 次多项式根的重数
是以下多项式的一个根. 求它的重数.
3 次含参数多项式的重根
求
的一个值使以下多项式有一个重根, 并求出这个重根.
警告. 本练习的回答中不能有近似数! 解都是整数. 找找看.
4 次含参数多项式的重根
求
的一个值使以下多项式有一个重根, 并求出这个重根.
警告. 本练习的回答中不能有近似数! 解都是整数. 找找看.
2次参数方程
参数 取什么实数值时, 多项式 ()2 + (2) + 有? (假设 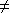 0.)
0.)
2次参数方程 II
参数 取什么实数值时, 多项式 ()2 + () + () 有一个根 ? (假设 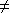 0.)
0.)
2次多项式的复根
求以下多项式的两个根 P() = 2 + () + (). 根 , 的次序可以任意.
2次多项式根的函数
设 , 是以下多项式的 2 个根 2 , 其中 是实数. 问 t = 2+2 的值是什么? (这个值是 的函数.)
3次多项式根的函数
设 , , 是以下多项式的 3 个根 3 2 , 其中 是非零实数. 问 t = 的值是什么? (这个值是 的函数.)
2次多项式根的实部
设 P() = 2 + 是有一对共轭复根的实系数多项式. 问根 r 的实部是什么?
用导数计算根的个数
设 P(x) 是 次系数多项式, 且设 P'(x) 是 P(x) 的导数. 已知 gcd(P(x),P'(x)) 是一个 次多项式. 问 P(x) 的不同的根的个数是多少? (包括实根与复根)
复合多项式的根
设 () 是多项式, () = 2 是另一多项式. 考虑复合多项式 (()) 和 (()). 填空: 若 是 的一个根, 则.
2次多项式的实根
求以下多项式的两个根 r1, r2
2 . (根是实数, 次序不计.)
和或积的根的重数
设 () 和 () 是两个多项式. 填空: 若 是 () 的 重根也是 () 的 重根, 则 是 的 ________ 重根.
2次多项式根的情况
以下二次多项式有怎样的根? 2
三项式的因式分解
因式分解
.
第 1 步. 你把
项化成完全平方:
= (
)2.
我们有
.
第 2 步. 所以
所以
第 3 步.
现在我们应用公式
(
)(
).
结果:
.
(你应该输入化简后的表达式.)
3次多项式的三重根
在以下多项式里参数 和 取什么实数值时会有三重根 P() = 3 + 2 + + (-) ?
3次多项式的三重根 II
在以下多项式里参数 和 取什么实数值时会有三重根 P() = 3 2 +(++) ? (可有多个解.)
The most recent version
由于 WIMS 不能识别您的浏览器, 本页不能正常显示.
请注意: WIMS 的网页是交互式的: 它们不是通常的 HTML 文件. 只能在线交互地
使用. 您用自动化程序收集的网页是无用的.
- Description: 关于实或复系数单变量多项式的一组练习. interactive exercises, online calculators and plotters, mathematical recreation and games
- Keywords: interactive mathematics, interactive math, server side interactivity, algebra, polynomial,root,euclidean division,gcd,lcm,complex number
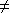 0.)
0.)
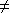 0.)
0.)
 0.)
0.)