| De grafiek van
is gedefinieerd op het domein  =
[- ,]
[- ,[ =
[- ,]
[- ,[  ] , ] ] , ]
en weergegeven in het vlak (O ; I, J) . Beantwoord de volgende vragen over de grafiek van
.
- Hoeveel oplossingen heeft de vergelijking
in
 ? ?
- De vergelijking
heeft geen oplossingen in het domein
 . .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft geen oplossing in het domein
 . .
De functie
is niet gedefinieerd in .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft één oplossing
1 op het domein
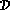 . .
De waarde van
1 op twee decimalen afgerond is .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft één oplossing
1 op het domein
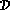 . .
De functie
is niet gedefinieerd in .
De waarde van
1 afgerond op 0.1 nauwkeurig : .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft één oplossing
1 op het domein
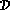 . De functie
is niet gedfinieerd in . . De functie
is niet gedfinieerd in .
De waarde van
1 afgerond op 0.1 nauwkeurig is : .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft twee oplossingen
1 en
2 op het domein
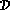 . .
De afgeronde waarden van
1 en
2 zijn respectievelijk : en .
- Maak het tekenverloop van
in de tabel af :
- De vergelijking
heeft op het domein
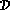 drie oplossingen
1,
2 en
3 . drie oplossingen
1,
2 en
3 .
De op 0.1 nauwkeurig afgeronde waarden van
1,
2 en
3 zijn respectievelijk : , en . - Maak het tekenverloop van
in de tabel af :
|
xrange -, yrange , parallel -,,-,,1,0, 2*+1, grey parallel -,,,,0,1, (-)++1, grey hline 0,0,black vline 0,0,black arrow 0,0,1,0,8, black arrow 0,0,0,1,8, black text black , -0.5,-0.2,small , O text black , 1,-0.3,small , I text black , -0.5,1,small , J linewidth 1.5 plot blue,
|
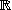 door
.
door
. 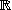 door
.
door
. 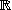 door:
is in
door:
is in  altijd:
altijd:
 voor alle
voor alle
 uitgezonderd
,
door
uitgezonderd
,
door