LA COMPLEXITÉ ÉLÉMENTAIRE étudiée sur QUELQUES ALGORITHMES CLASSIQUES
INTRODUCTION
Après avoir analysé un problème posé et trouvé un algorithme permettant de le résoudre, on désire bien souvent avoir une idée: sur le temps d'exécution, sur la place occupée en mémoire ou sur un autre paramètre (exemple: distance totale parcourue par la tête d'une table traçante).
Par exemple, pour un algorithme concernant une application graphique élémentaire, le temps d'exécution de l'algorithme est souvent lié au nombre de points à afficher et la place occupée en mémoire est liée à la taille de l'écran.
La connaissance du temps d'exécution et de la place occupée en mémoire par l'algorithme se fait en calculant ce que l'on appelle la complexité en temps et la complexité en place de l'algorithme.
CALCUL DES COMPLEXITES EN TEMPS ET EN PLACE
Les complexités en temps et en place s'expriment en fonction d'un nombre N qui est lié aux données.
Ainsi, calculer la complexité en place d'un algorithme consiste souvent (sauf exception exemple: allocation implicite d'un espace mémoire) à compter le nombre de variables (indicées ou non) utilisées dans l'écriture de l'algorithme, et ainsi en déduire la place occupée en mémoire.
Le calcul de la complexité en temps consiste, lui, à trouver une fonction f dépendante de N telle qu'il existe une constante c permettant de majorer le temps d'exécution TPS (donc trouver c tel que TPS < c.f (N) ).
On dira alors que la complexité en temps de l'algorithme est de l'ordre de f (N) et on notera: complexité O ( f (N) ).
Remarques:
- En règle générale, la constante c est difficilement calculable et dépend de la machine et du langage utilisés. Dans certain cas particuliers (langage machine, langage d'assemblage) on peut alors calculer cette constante c avec précision.
- Le calcul de la complexité en temps et en place est surtout utile lorsque l'on a trouvé deux algorithmes pour résoudre un problème posé. Dans ce cas la comparaison des complexités nous permet de choisir le l'algorithme le plus adapté.
- Lorsque f(N) s'exprime sous la forme d'un polynôme (on plus généralement d'une expression dans laquelle interviennent des termes exponentiels ou logarithmiques dépendants de N) seul le terme de plus haut degrés (ou exponentiel) sera retenu pour exprimer la complexité en temps.
Exemples:
f(N) = apNp + ap-1Np-1 + + a1N + a0 donne une complexité de O (Np)
f(N) = a 2N + b Nk donne une complexité de O (2N)
f(N) = a Nk + log2N donne une complexité de O (Nk)
Le fait de connaître les complexités en temps et en place de différents algorithmes, résolvant le même problème, va nous permettre de répondre à des questions classiques du type: Quel est le meilleur algorithme?
Ainsi, suivant la machine utilisée (problème de taille mémoire) un algorithme sera considéré comme meilleur qu'un autre si sa complexité en place est plus faible on bien si son temps d'exécution est plus performant.
De manière générale, on cherchera surtout à optimiser la complexité en temps (même au détriment de la complexité en place).
A titre indicatif, voici un tableau comparatif de cinq algorithmes dont les complexités en temps sont respectivement O (N), O (Nlog2N), O (N2), O (N3), O (2N). La machine utilisée est supposée traiter 1.000.000 de "cas" par seconde. Nous trouvons alors dans le tableau le nombre de données traitables en 1 seconde, 1 minute, 1 heure et à titre (très indicatif) 1 mois. Ne seront intéressants dans ce tableau que les nombres inférieurs à 106 (les valeurs supérieurs ne représentant pas un nombre raisonnable de données à traiter)
|
Nombre de données pouvant être traitées en: | |||
| 1 seconde | 1 minute | 1 heure | 1 mois | |
| N | 1.000.000 | 6.107 | 36.108 | 26.1011 |
| Nlog2N | 62.500 | 28.105 | 13.107 | 72.109 |
| N2 | 1.000 | 7.746 | 60.000 | 16.105 |
| N3 | 100 | 391 | 1.532 | 13.736 |
| 2N | 20 | 26 | 31 | 42 |
Dans la suite de ce chapitre nous allons, à l'aide d'exemples, comparer différents algorithmes résolvant le même problème et choisir, après calcul de leur complexité en temps, celui qui semble le meilleur.
EXEMPLE 1: Recherche d'un élément dans un tableau trié
1) 1er Algorithme (élémentaire) la recherche séquentielle
Principe: On compare l'élément cherché avec tous les éléments du tableau, un drapeau indiquera si l'élément cherché est existant ou non.
Comparer X (élément cherché) avec T[1], puis avec T[2] etc...
L'algorithme peut alors s'exprimer sous la forme de la procédure suivante:
Si on suppose que:
| L'instruction: | prend un temps: |
| afficher 'élément à chercher' | A1 |
| lire X | U1 |
| DRAP <-- FAUX | K1 |
| si T[ I ] = X alors ... | K2 |
| si DRAP alors afficher... | A2 |
On obtient alors:
f(N) = A1 + U1 + K1 + K2 * N + A2
Remarque: les temps Ai dépendent de la rapidité de l'affichage (et donc du matériel) et les temps Ui dépendent de l'Utilisateur. Ces temps ne dépendent donc pas de l'algorithme lui-même, la fonction représentant le temps d'exécution de l'algorithme va donc se réduire à: f(N) = K1 + K2 * N
D'où, la complexité en temps de cet algorithme est: O (N)
Essai d'amélioration
Lors de la recherche séquentielle, si l'élément X est trouvé, alors il est inutile de poursuivre la recherche. De plus si lors d'une comparaison X est inférieur à la donnée du tableau alors X ne peut pas se trouver dans celui-ci d'où la recherche peut à nouveau être interrompue.
On peut alors écrire l'algorithme sous la forme:
Ici se pose le problème du calcul de la complexité en temps. En effet, en observant le programme, il est difficile de connaître le nombre de fois où l'instruction 'comparaison' est exécutée (celle-ci étant dans une boucle indéfinie).
Ainsi, pour calculer la complexité en temps d'un tel algorithme, on doit examiner la façon dont il a été construit (revenir sur le principe même de l'algorithme). Par ailleurs, suivant les données, le temps d'exécution d'un tel algorithme sera variable.
Ceci nous permet d'introduire de nouvelles notions: le temps moyen d'exécution (ou cas moyen), le pire des cas et le cas favorable.
![]()
| Cas favorable | recherche de 3 | 1 comparaison |
| Pire des cas | recherche de 26 ou 40 (inexistant) | 8 (=N) comparaisons |
| Cas moyen | moyenne des cas (admis) | N/2 comparaisons |
Remarque:
Bien que la complexité en temps ne soit pas améliorée par l'introduction des différents tests d'arrêt, il est évident que cette écriture améliore le travail de recherche.
2) 2ème Algorithme la recherche par dichotomie
Principe: Eliminer en une comparaison la moitié des données susceptibles d'être l'élément cherché, ainsi le problème se réduira à chercher un élément parmi N/2 données. Pour cela on compare l'élément cherché avec l'élément situé au milieu du tableau. Si celui-ci est identique alors l'élément cherché existe; sinon, si l'élément cherché est plus petit que l'élément "milieu" alors si cet élément existe il doit nécessairement se trouver dans la première partie du tableau, on peut donc effectuer une recherche dans cette partie. De façon symétrique, si l'élément cherché est plus grand que l'élément "milieu" on effectuera une recherche dans la deuxième partie du tableau.
Exemple: Soit le tableau T suivant:
![]()
On va rechercher deux éléments (l'un existant l'autre non) et observer le déroulement de la recherche et le nombre de comparaisons nécessaire pour obtenir le résultat.
Calcul de la complexité en temps de cet algorithme
Là encore, ayant à considérer une boucle indéfinie (simuler par une procédure récursive(voir la solution de l'exercice 1), il est difficile de calculer directement la complexité en temps de l'algorithme en observant le programme. Il faut donc examiner la façon dont l'algorithme a été construit.
Après chaque comparaison le nombre de données, restant à considérer, est divisé par 2 (éventuellement N/2 - 1 données suivant la parité de N). Ainsi:
| après | 1 | comparaison | il reste | N/2 | données à considérer |
| après | 2 | comparaisons | il reste | N/22 | données à considérer |
| ! | ! | ! | ! | ! | ! |
| ! | ! | ! | ! | ! | ! |
| après | k | comparaisons | il reste | N/2k | données à considérer |
| après | k + 1 | comparaisons | il reste | N/2k+1 | données à considérer |
| ! | ! | ! | ! | ! | ! |
EXEMPLE 2: Calcul du Nième terme de la suite de Fibonacci
Nous avons déjà rencontré cette suite dans le chapitre1. Nous allons ici, examiner la complexité des algorithmes déjà trouvés.
1) 1er Algorithme ("élémentaire (pour l'écriture)")
De la même façon que pour une boucle indéfinie, il est difficile de calculer la complexité d'un algorithme lorsque celui-ci est exprimé sous la forme d'une procédure (ou fonction) récursive.
La complexité de l'algorithme dépend ici du nombre d'appels fait à la fonction (car il n'y a pas d'autre opération que les appels à la fonction à l'intérieur de celle-ci).
Calculons, pour exemple, le nombre d'appels nécessaire au calcul du cinquième terme de la suite de Fibonacci. Pour cela, on va dessiner l 'arbre' des appels.
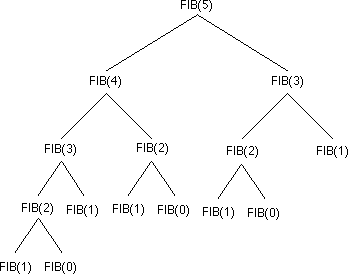
On observe alors ici 14 appels à la fonction (en dehors de l'appel initial).
Le nombre d'opérations (complexité de l'algorithme) est donc lié au nombre de noeuds existant dans un arbre binaire de hauteur N. On admettra que les noeuds manquant (pour que l'arbre binaire soit équilibré) n'interviennent pas dans le calcul de la complexité.
On obtient donc une complexité de: O (2N )
2) 2ème Algorithme
Principe: Dans le premier algorithme, les différents termes de la suite sont calculés plusieurs fois au cours du calcul de F(N) (exemple: pour N = 5 F(1) est calculé 5 fois). Il suffit donc de mémoriser les différentes valeurs des termes qui précèdent F(N). Pour cela on calcule F(N) en commençant par calculer les premiers termes de la suite.
On peut alors exprimer cet algorithme sous la forme suivante:
La complexité de cet algorithme est alors: O (N)
Remarque: Passage d'une procédure récursive à une procédure non récursive.
Dans la plupart des cas, l'utilisation d'une procédure récursive est coûteuse en temps et on peut se demander s'il n'existe pas une procédure non récursive résolvant le même problème. Deux cas peuvent alors se présenter.
1er Cas: Il existe un algorithme itératif permettant de résoudre le problème. On peut alors écrire la procédure itérative correspondante; et, en règle générale, la complexité se trouve ainsi améliorée.
2ème Cas: Il n'existe pas (ou on n'a pas encore trouvé) d'algorithme itératif. On peut alors écrire une procédure qui simule la récursivité à l'aide de piles. Dans ce cas la complexité reste inchangée et seul le temps d'exécution est éventuellement amélioré. Toutefois, il est souvent délicat d'écrire une telle procédure.
EXEMPLE 3: Tri d'un tableau T
Remarque: On supposera que les éléments du tableau sont des entiers et que l'on désire les trier par ordre croissant.
2) 2ème Algorithme Un Tri par INSERTION
Calcul de la complexité:
Ici, encore il faut revenir à l'algorithme lui-même pour calculer la complexité. Si on suppose que tous les éléments sont distincts, alors on peut assimiler le tableau initial à une permutation de l'ensemble des données composant le tableau trié. Ainsi, le nombre de fois, qu'est effectué l'affectation T[J + 1] <-- T[J], est égal au nombre d'inversions pour réaliser la permutation (nombre de Tj tels que Tj > Ti i < j). Cette valeur est en moyenne de:
D'où une complexité de O(N2)
3) 3ème Algorithme Le Tri QUICKSORT
Idée: Si on peut répartir les éléments du tableau T dans deux tableaux T1 et T2 de N/2 éléments, de telle sorte que les éléments du tableau T1 soient inférieurs aux éléments du tableau T2; alors il suffira de trier les tableaux T1 et T2 puis de les "réunir" pour reconstituer le tableau T trié.
Principe: Lorsque l'on considère un élément du tableau T il faut pouvoir décider de le mettre dans le tableau T1 ou dans le tableau T2. Une telle décision n'est possible que si l'on peut comparer cet élément avec un élément "milieu" du tableau. Or connaître l'élément "milieu" du tableau T puis les éléments "milieux" des tableaux T1 et T2 etc, revient à connaître le tableau T trié.
On va donc devoir faire le choix arbitraire d'un élément (appelé PIVOT) du tableau T et construire les tableaux T1 et T2 en supposant que cet élément est l'élément "milieu" du tableau T.
Choix du pivot: On va prendre, de façon arbitraire, le dernier élément du tableau.
Mise en place du pivot et construction des tableaux T1 et T2.
Ces opérations vont se faire en une seule exploration du tableau T. De plus, pour ne pas créer en mémoire de structures T1 et T2 inutiles, ces tableaux seront en fait des sous tableaux de T.
Pour cela on se munit d'un pointeur gauche G, pointant sur le 1er élément du sous tableau considéré (initialement le tableau T entier), et d'un pointeur droit D pointant sur l'élément précédant le pivot dans le sous tableau considéré.
![]()
On incrémente ensuite le pointeur G tant que T[G] < Pivot (ce qui empêche le pointeur D de dépasser le pivot (les éléments égaux au pivot seront donc dans le sous tableau T2)), puis on décrémente le pointeur D tant que T[D] > Pivot (pour stopper la progression du pointeur D il faudra donc initialiser une case fictive d'adresse 0 avec la valeur - ("l'infini") (prendre la plus petite valeur accessible sur la machine)). On échange alors les éléments pointés par D et G puisque chacun de ces éléments se situe du mauvais coté dans le tableau, puis on recommence jusqu'à ce que les pointeurs G et D se soient croisés.
échange puis déplacements des pointeurs
échange puis déplacements des pointeurs
échange puis déplacements des pointeurs
On échange alors le pivot avec l'élément pointé par G
2ème étape: On recommence sur les sous tableaux
choix des pivots
Placements des pivots et constitution de quatre sous tableaux (ici l'un d'entre eux est vide).
3ème étape
4ème étape
Reste un sous tableau à un élément (10): le tableau T est donc trié.
Calcul de la complexité:
Observons les différents appels à la procédure. Pour cela, supposons que N peut s'écrire sous la forme 2k et qu'à chaque étape les sous tableaux considérés sont bien coupés en deux sous tableaux contenant chacun le même nombre d'éléments.
On peut représenter les différents appels de la procédure donnée dans la solution de l'exercice 3, sous la forme de l'arbre suivant: (on notera les bornes des sous tableaux à l'appel de la procédure)
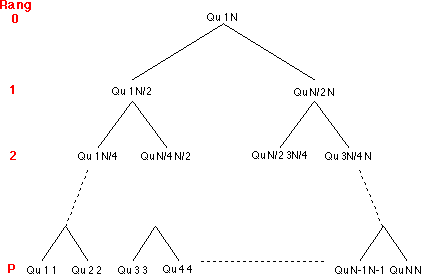
Calculons le nombre d'opérations nécessaires pour placer les différents pivots (nombre d'opérations pour trier le tableau).
pour passer du rang 0 au rang 1 N opérations pour placer le pivot pour passer du rang 1 au rang 2 2 * (N/2) = N opérations pour placer les 2 pivots | | | | | | | | | | | | pour passer du rang i au rang i+1 2i * (N/2i) = N opérations pour placer les 2i pivots | | | | | | | |
D'où le nombre d'opérations nécessaire pour trier le tableau est:
N * (nombre de rangs) = N * P = N * log2N
Cas défavorable:
Cas moyen:
On admettra que le nombre d'opérations dans la moyenne des cas reste, comme pour le cas favorable, de l'ordre de N * log2N (idée: on a plus de "chance" de trouver un tableau désordonné plutôt qu'un tableau ordonné).
La complexité de l'algorithme Quicksort est donc O(N * log2N).
Remarques:
- On peut améliorer le choix du pivot de différentes façons. Exemple: prendre l'élément "moyen" parmi T[D] , T[F] , T[(D+F)%2].
- Plus les sous tableaux sont petits et plus ils ont de "chance" (plus grande probabilité) d'être triés. De plus l'appel récursif coûte cher en temps. D'où lorsque les sous tableaux seront de petites tailles on passera à un autre algorithme de tri (exemple: le tri par insertion vu précédemment).
EXERCICES sur la Complexité
Élémentaire
Auteur: Philippe Moreau (U.P.J.V.)