-
 |
 CHAPITRE 2
CHAPITRE 2
|
-
- auteur: Philippe
Moreau (U.P.J.V.)
-
- Si vous avez déjà lu le chapitre vous pouvez accéder
à la série d'EXERCICES
concernant les structures de données linéaires.
- Ces exercices sont également accessibles à la fin du
chapitre.
LES ARBRES BINAIRES - PARCOURS
et RECHERCHE
- Définition:
- On appelle arbre binaire de type T une
structure formée:
- - d'un élément appelé racine
- - et d'un ensemble d'au plus 2 arbres de types T, aussi appelés
sous-arbres.
-
- Exemples:
-
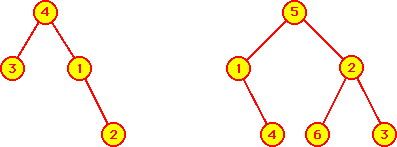
-
- VOCABULAIRE
- On constate que la représentation d'un arbre peut prendre une
forme particulière (sorte d'arbre dessiné à l'envers).
Ainsi les sommets prendront également des noms particuliers.
- par analogie à l'arbre (au sens naturel du terme) on parlera
de:
- noeuds, racine, feuilles, branches
-
- et par analogie à l'arbre généalogique on parlera
de:
- pères, fils, frères
-
- ainsi, sur le deuxième arbre pris en exemple:
- 5 est la racine
- 4, 6, 3 sont des feuilles
- 1 , 2, 3, 4, 5, 6 sont des noeuds
- 2, 3, 6 appartiennent à la même branche
- de même on dira que:
- 2 est le père de 6
- 1 est le fils de 5
- 1et 2 sont frères
-
- Remarque: Dans un arbre binaire, le fils unique d'un
noeud ne sera jamais placé à l'aplomb de son père,
mais toujours dirigé soit vers la gauche soit vers la droite. On
parlera alors de fils droit et de fils gauche ou encore de
sous arbre droit et de sous arbre gauche. (exemple: 4 et
1 sont dans le même sous arbre gauche issu de 5)
-
-
- IMPLANTATION EN MEMOIRE
-
- Informations nécessaires: pour un noeud quelconque de l'arbre
binaire, les seules informations nécessaires sont:
- - l'information sur son nom
- - les informations concernant ses fils.
-
- On peut alors décider que pour chaque noeud on construit un
article du type:

- L'arbre binaire suivant:
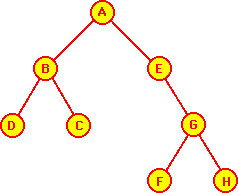
- sera alors représenté par:
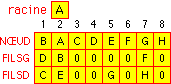
- de plus il faut avoir une indication sur la racine (ici RACINE = A).
-
-
- On constate que, dans ce type de représentation, il est difficile
d'accéder au petit fils d'un noeud (parcours du tableau NOEUD pour
trouver où se trouve le fils). Pour résoudre se problème
on décidera plutôt de construire un article du type:

- Ainsi l'arbre ci-dessus pourra se représenter par le chaînage
suivant:
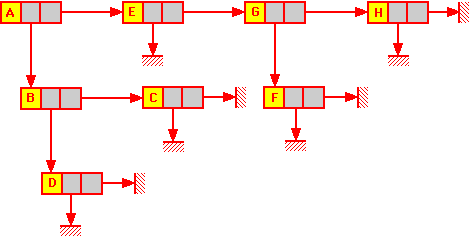
- ce qui pourra s'implanter en mémoire sous la forme:
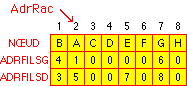
- avec ADRRAC = 2
-
-
-
- PARCOURS D'UN ARBRE BINAIRE
-
- Lorsque l'on désire connaître les informations contenues
dans un arbre (valeurs ou contenus de ses noeuds), cela nécessite
de parcourir (ou visiter) celui-ci. Pour cela il existe différentes
méthodes pour effectuer la visite d'un arbre binaire. Principalement,
nous en retiendrons trois qui sont: les méthodes de visites dites
preorder, inorder et postorder.
-
-
- Principe de ces visites:
-
- Visite preorder:
- - on visite la racine (prise en compte de l'information)
- - on visite le sous arbre gauche (SAG)
- - on visite le sous arbre droit (SAD)
-
- Visite inorder:
- - on visite le sous arbre gauche (SAG)
- - on visite la racine (prise en compte de l'information)
- - on visite le sous arbre droit (SAD)
-
- Visite postorder:
- - on visite le sous arbre gauche (SAG)
- - on visite le sous arbre droit (SAD)
- - on visite la racine (prise en compte de l'information)
-
- Il est clair que ces trois principes de visites font appel à
la récursivité. Ainsi, on appliquera ces mêmes principes
pour les visites des sous arbres gauches et droits mentionnés.
-
-
- Exemple 1:
- Observons sur l'arbre binaire suivant le résultat des différentes
visites.
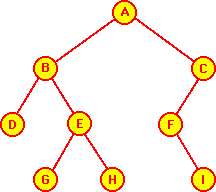
-
- Ainsi, pour la visite preorder, l'ordre dans lequel les sommets
seront pris en considération est:
- A B D E G H C F I
-
- Pour la visite inorder, l'ordre dans lequel les sommets seront
pris en considération est:
- D B G E H A F I C
-
- Enfin, pour la visite postorder, l'ordre dans lequel les sommets
seront pris en considération est:
- D G H E B I F C A
-
-
-
- Remarque:
-
- Le sens de parcours de l'arbre binaire est le même dans les trois
cas. Seul change, dans la visite, l'instant de prise en considération
de l'information au moment du parcours. Ainsi, on peut tracer le chemin
parcouru dans l'arbre:
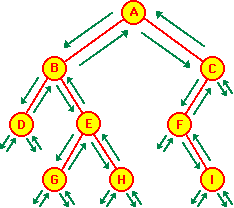
-
-
- Pour connaître la liste des informations rencontrées il
suffit de savoir à quel moment le noeud est visité.
- En marquant d'un · l'endroit où
se situe la visite d'un noeud il suffit alors de remplacer:
| Pour PREORDER |
 |
par |
 |
| Pour INORDER |
 ou ou |
par |
 ou ou |
| Pour POSTORDER |
 |
par |
 |
-
- Exemple 2:
-
- Dans l'arbre suivant, les informations (contenu des nuds) sont des
opérations, fonctions, nombres ou identificateurs.
- Observons alors les résultats obtenus après utilisation
des différentes méthodes de parcours sur un tel arbre binaire.
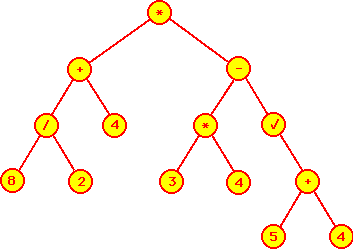
-
- Ainsi, après un parcours preorder, on obtient:
- * + / 8 2 4 - * 3 4
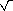 + 5 4
+ 5 4
-
- Après un parcours inorder, on obtient:
- 8 / 2 + 4 * 3 * 4 -
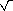 5 + 4
5 + 4
-
- Enfin, après un parcours postorder, on obtient:
- 8 2 / 4 + 3 4 * 5 4 + ÷
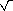 - *
- *
-
- Ajoutons les règles suivantes pour les lectures preorder et
inorder:
- - Lorsque l'on descend dans un sous arbre on ouvre une parenthèse
- - Lorsque l'on remonte d'un sous arbre on ferme une parenthèse
- On obtient alors:
- Pour preorder
- * (+ (/ (8) (2)) (4)) (- (* (3) (4)) (
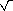 (+ (5) (4))
) )
(+ (5) (4))
) )
-
- Pour inorder
- ( ((8) / (2)) + (4) ) * ( ((3) * (4)) - (
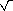 ((5) + (4)))
)
((5) + (4)))
)
-
-
- On s'aperçoit alors que si l'on interprète le résultat
obtenu lors de la visite inorder, comme étant l'écriture
d'une expression algébrique (écriture dite infixée);
le résultat obtenu après une lecture preorder correspond
à l'écriture préfixée (sous forme de liste)
de la même expression et le résultat de la lecture postorder
correspond à l'écriture postfixée de l'expression
(cf exemple de manipulation sur les piles CHAP II).
- Rappelons à titre d'exemple que le langage FORTH utilise l'écriture
postfixée sous cette forme et que le langage LISP utilise l'écriture
préfixée.
ARBRE BINAIRE DE RECHERCHE
-
- Un arbre binaire de recherche est un arbre binaire possédant
récursivement la propriété suivante:
-
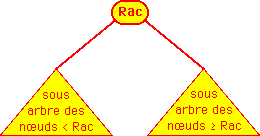
- Les noeuds du sous arbre gauche sont tous inférieurs à
la racine, elle-même inférieure aux noeuds du sous arbre droit
(les éléments égaux pouvant être arbitrairement
placés à gauche ou à droite (choix à faire)).
-
- Ce qui se visualise de la façon suivante:
-
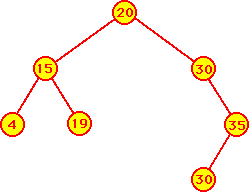
- Exemple:
-
- Remarque:
- Ainsi que son nom l'indique, cet arbre est particulièrement
utile pour résoudre les problèmes de recherche d'un noeud
dans un arbre. En effet, si X est l'élément cherché,
il suffit de comparer celui-ci avec la racine pour éliminer tous
les candidats se trouvant dans le sous arbre gauche ou dans le sous arbre
droit (en fonction du résultat du test avec la racine).
-
-
- Création d'un arbre binaire de recherche:
-
- Soit une suite S[1] , S[2] , , S[N] d'éléments. On désire,
à partir de ces éléments, créer un arbre binaire
de recherche.
-
- Principe:
- On réalise alors des insertions successives de chacun des éléments
dans un arbre binaire de la manière suivante:
- - S[1] (premier élément considéré) est
la racine de l'arbre
- - si S[i] est inférieur à la racine alors on insère
S[i] dans le sous arbre gauche.
- - si S[i] est supérieur ou égal à la racine alors
on insère S[i] dans le sous arbre droit.
-
-
- Exemple:
-
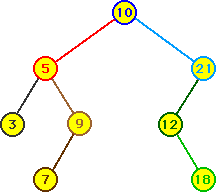
- Soit:
- 10 , 21 , 5 , 12 , 18 , 9 , 3 , 7 la suite d'éléments
considérés, alors on créera, par l'insertion successive
des éléments, l'arbre binaire de recherche suivant:
insertion de 10
insertion de 21
insertion de 5
insertion de 12
insertion de 18
insertion de 9
insertion de 3
insertion de 7
|
 |
-
-
- EXERCICES sur les Arbres Binaires
Auteur: Philippe Moreau
(U.P.J.V.)

![]()


![]()







